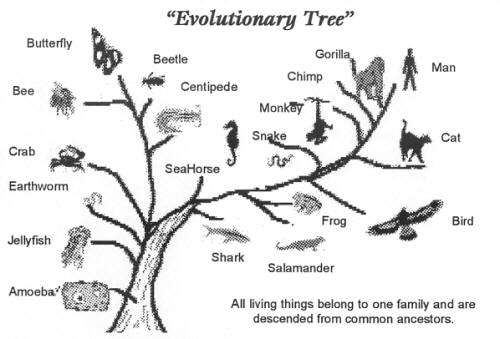
Dendogram

Dendrogram is best used for classification, probability, decision-making and hierarchy. These could be possible options, decision trees, probability growth, evolutionary growth, or generations. These are useful when it comes to determining how things differentiate while having certain things in common.

A dendogram needs to be visually efficient, in sense that it should display the information in the most visually pleasing way while not overwhelming the user with too much data or decisions.

Three particularly good examples include the following:

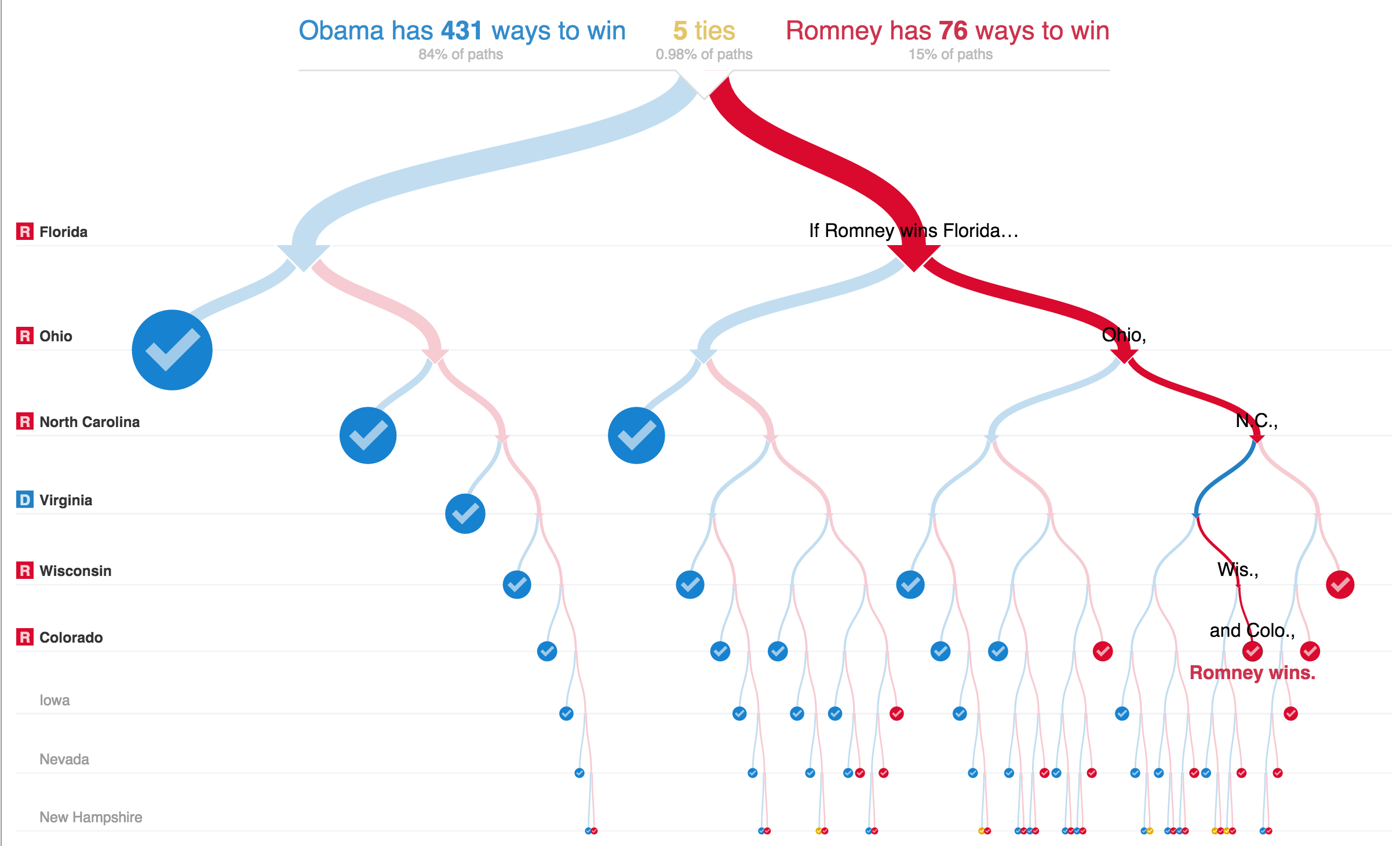
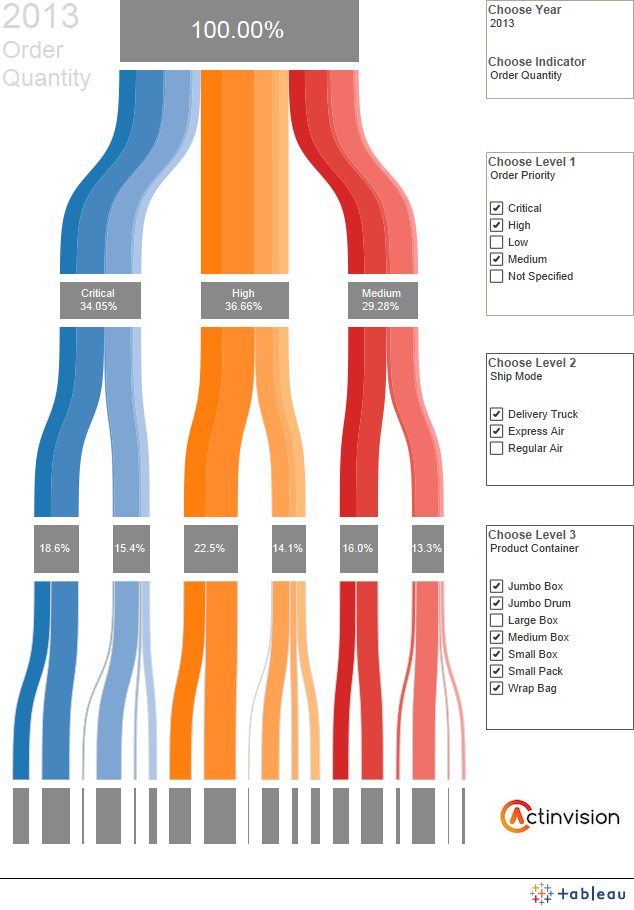
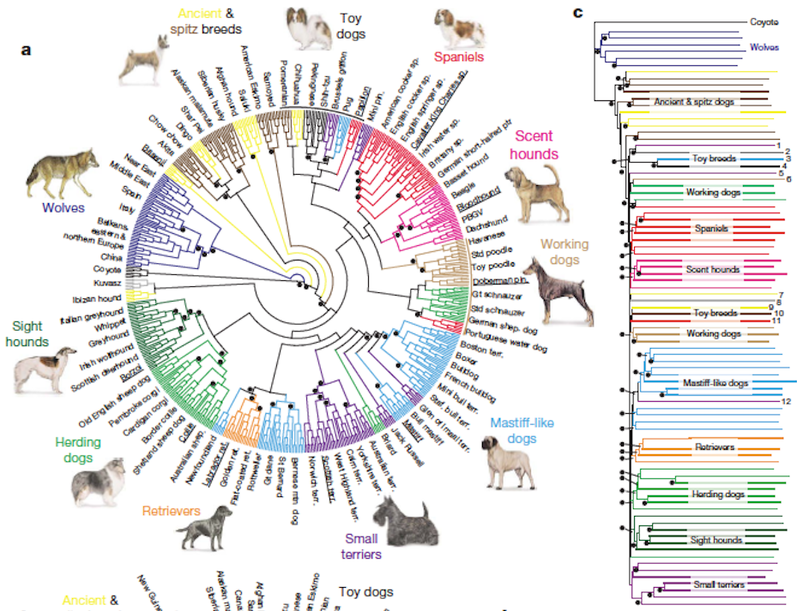
In number 4, despite being very data heavy, the information is presented spaced out enough not to overwhelm the user.

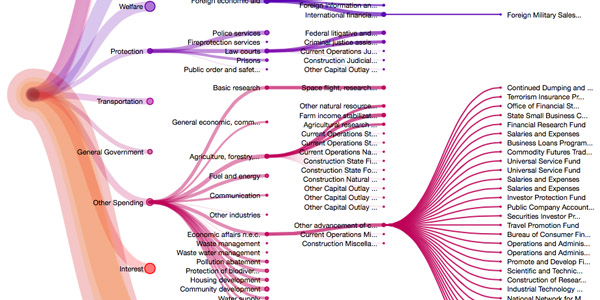
In this cases, there is too much information, but combined with the graph on the edge, it does overall redeem the graph.

Some bad examples include:
Too much information, not at all clear for the user.

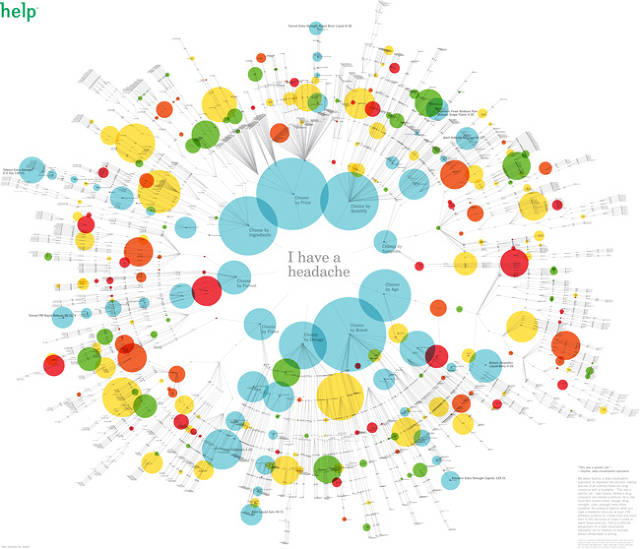
No classification, no information about the branches, and illegible writing.

Star Plots ⭐️

Star plots, sometimes called radar charts or web charts, are a graphic device method used to display multivariate data. Multivariate in this sense refers to the having of multiple characteristics to observe. The variables must also be ranged values.

Star plots are often used to display several different observations of the same type of data. For example, this set of star plots compares different car models in the same nine variables:

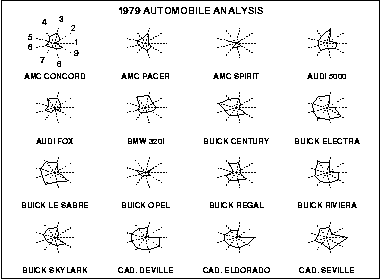
1. Price
2. Mileage (MPG)
3. 1978 Repair Record (1 = Worst, 5 = Best)
4. 1977 Repair Record (1 = Worst, 5 = Best)
5. Headroom
6. Rear Seat Room
7. Trunk Space
8. Weight
9. Length

Like many other star plots, labeling variables on the chart can be convoluting, so the variables are listed seperately above. In this set of plots, we can see that Cadillacs are the most expensive cars of the observed values.

This method of comparing similar items can be done on the same plot (rather than on separate axes) using different colors or line styles, as in the following. This method makes it easy to compare one observation to another, but can become difficult to read with a larger number of observations. Here, we can easily see that Design 1 (in green) has a strong dominance in mass, or an outlier.

A popular presentation of this data visualization method is in "personality type" analysis tests. Typically, there is no relationship between the placement of variables, but this chart made use of this spatial technique and grouped personality variables that are commonly related, into five groups, indicated by color:

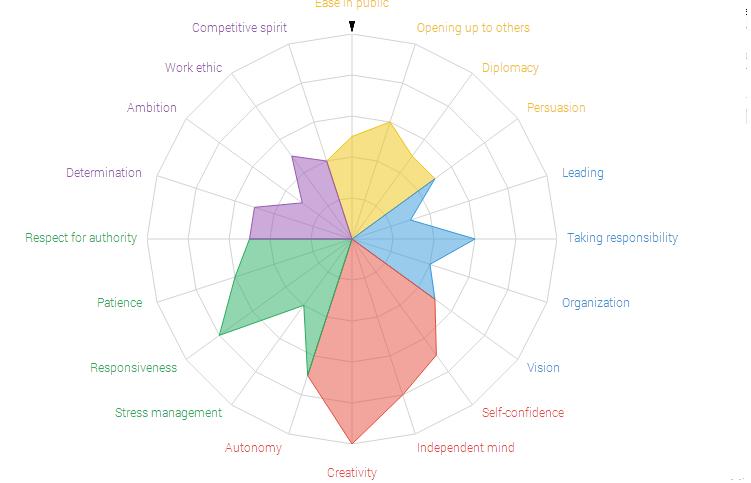
The star plot is useful in answering three major questions:

1. Which variables, if any, are dominant (or lacking) in a given observation?
2. What observations are similar? (i.e. Are there any trends between some or all observations?)
3. Are there any observations that are outliers?

It can also be used to show changes between discrete periods of time. The following graphic compares revenue of companies between two years. The years are marked as different observations by colored lines.

Note how this display is much easier to cognitively process than trying to mentally calculate differences in a tabular chart as in below.

Conversely, one can display the variables (the axes) as discrete times as well. The following graphic compares item stock by line/observations and labels the months as variables.

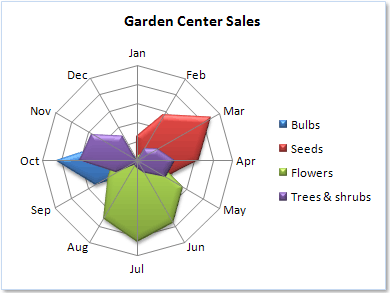
The main weakness of star plots is that they are limited to displaying a few variables at a time (practically speaking, no more than 20, but there are some that are as large as up to 100 variables). After that, the web becomes overwhelming or extremely large. The plot below is difficult to understand because of its sheer number of variables, obscurely labeled variables, and bad color choice (two types of blue for very similar observations).

Rubber Sheet

Like a heat map, but used to map four or more dimensions, through the use of a colored, three dimensional surface.

Example 1

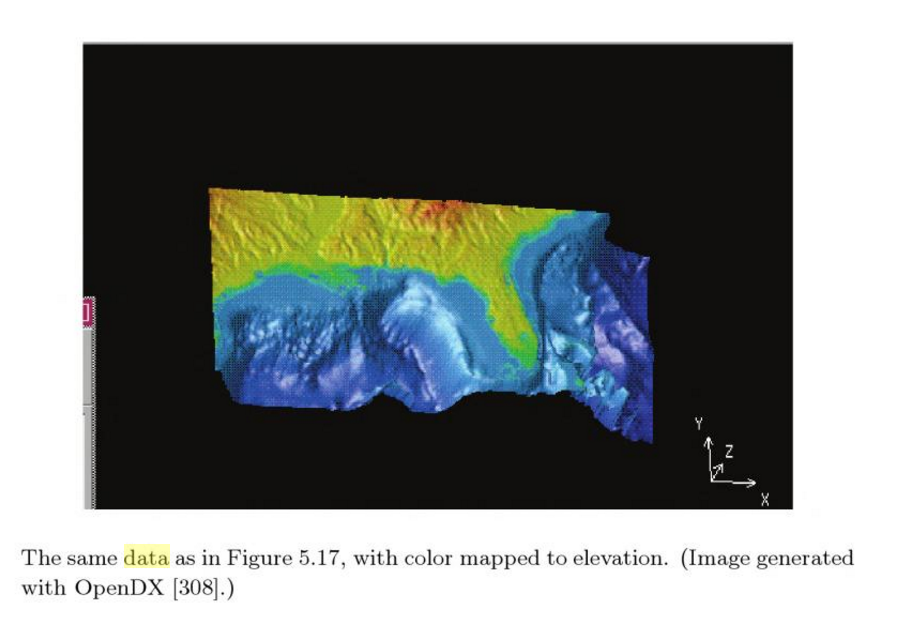
Example 2
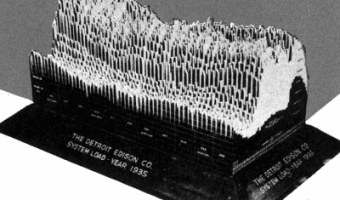
A large 3D physical visualization made by the Detroit Edison Company showing electricity consumption for the year 1935, with a slice per day and each day split into 30 min intervals.

physics data visualizations--> http://dataphys.org/list/

Linear and radial parallel coordinates

Parallel coordinates is a common way of visualizing high-dimensional geometry and analyzing multivariate data. Vertical bars represent each dimension. Each element of the data set has values for each dimension, which are shown as points along the vertical axis and then connected together.

Good parallel coordinates present clear

• Data structure • Data trend • Correlations

Good example 1:

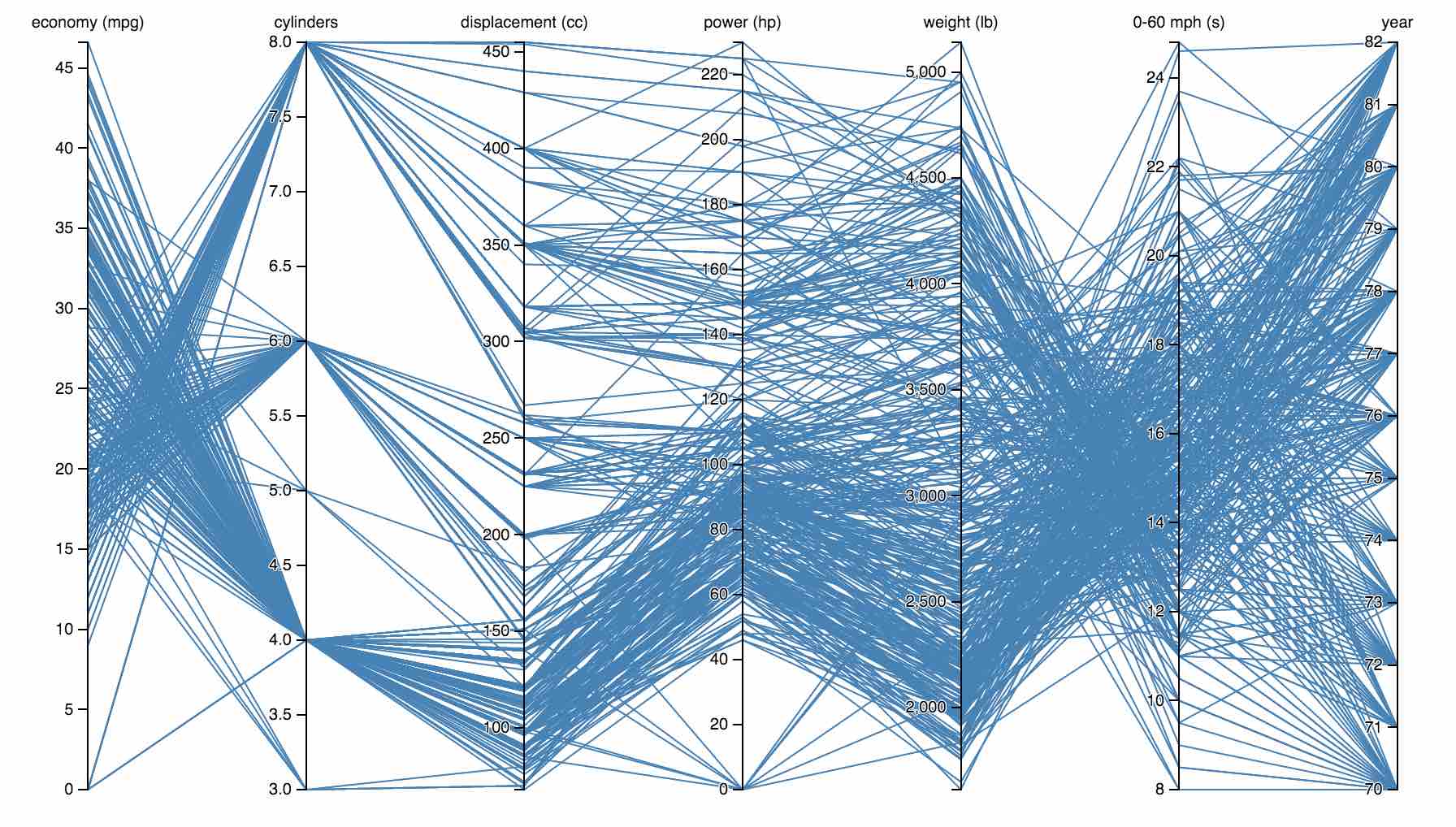
In the space between MPG and cylinders, you can tell that eight-cylinder cars generally have lower mileage than six- and four-cylinder ones. Just follow the lines and look at how they cross: lots of crossing lines are an indication of an inverse relationship, and that is clearly the case here: the more cylinders, the lower the mileage.

The correlation is much more direct between cylinders and horsepower: more cylinders means more horses. There are some crossing lines here as well, of course, so more cylinders do not always mean more power, but the general trend is clearly there.

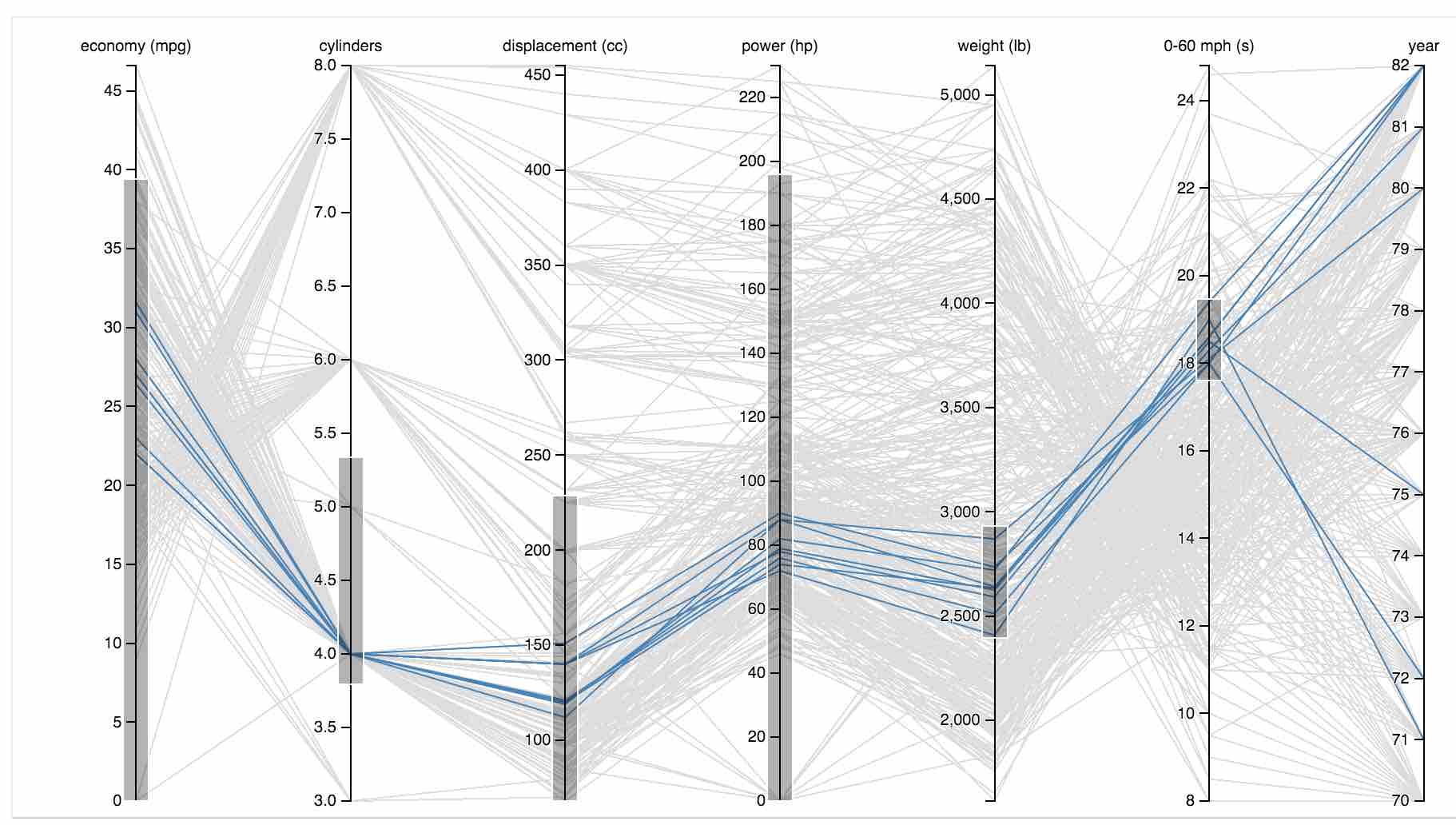
Good example 2:

Good example 3:

Radial parallel coordinates

A fairly large set of data is represented in a relatively small amount of space. If this were to be straightened out linearly the power and functionality would be lost. Within a small amount of visual space, many different stories are unfolding before our eyes. While we see that most information flows from the blue section highlighted, we also see very clearly that four sources come into it from the outside. Another quick understanding is that even though it seems to cover the most territory, the bar charts in the outermost ring shows us that relative to the other segments, the blue has the least activity in that only one bar of green stands out with a higher value. Even though we don’t know what this data represents, the quick inspection allows us to see relationships, and that’s what we’re after.

Most RCDs that I’ve come across so far are interactive. In this example, a hover over the blue fades out all the other segments so that you can concentrate on what relationships are shared by it.

Bad example 1:

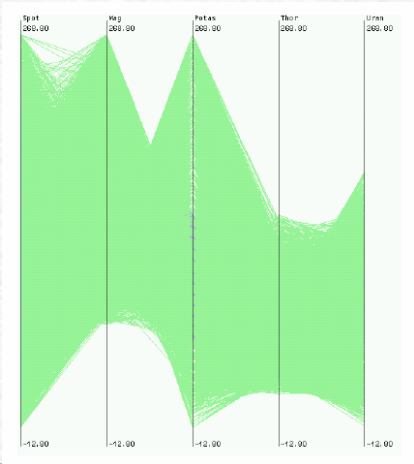
Bad example 2:

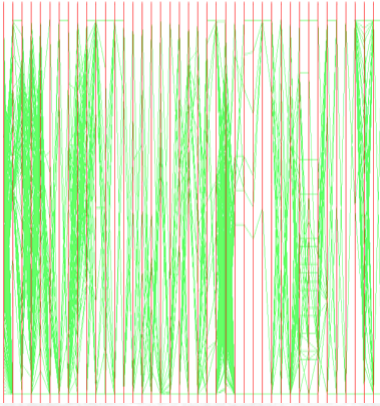
Bad example 3:

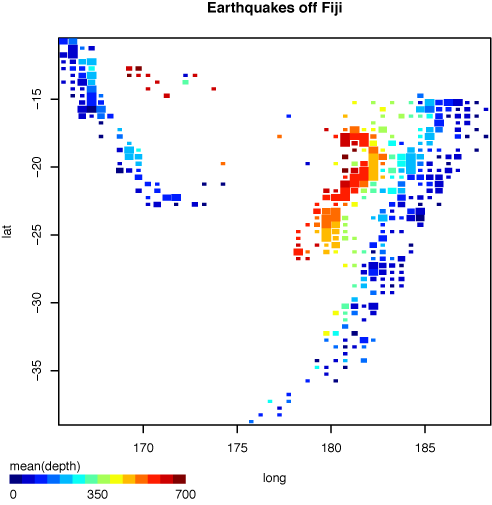
HEAT MAP

a graphical representation of data where the values contained in a matrix are represented as colors.

Can be used for understanding behaviors on multiple scales: digital, built environment, geography
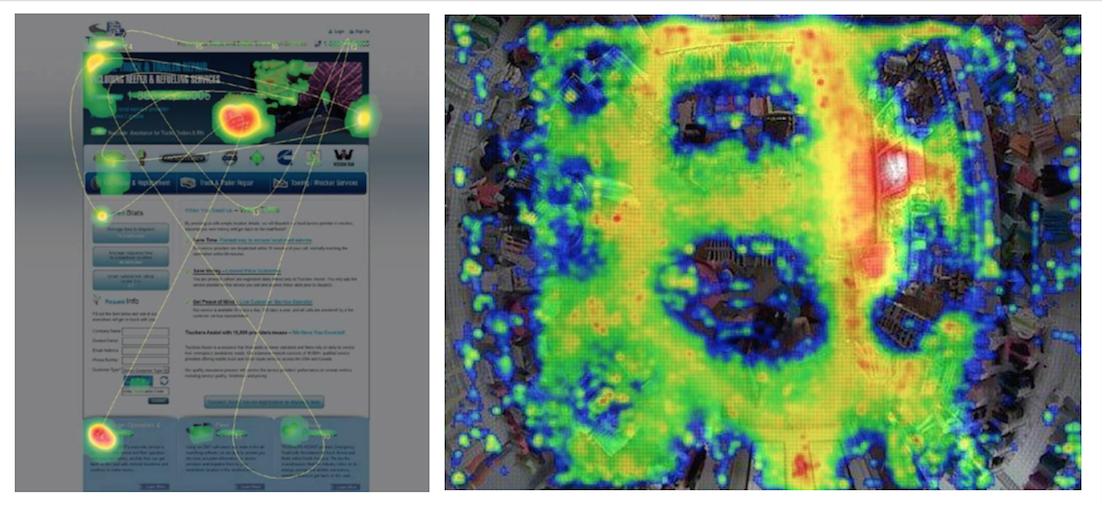
UI/UX, shopping, air traffic

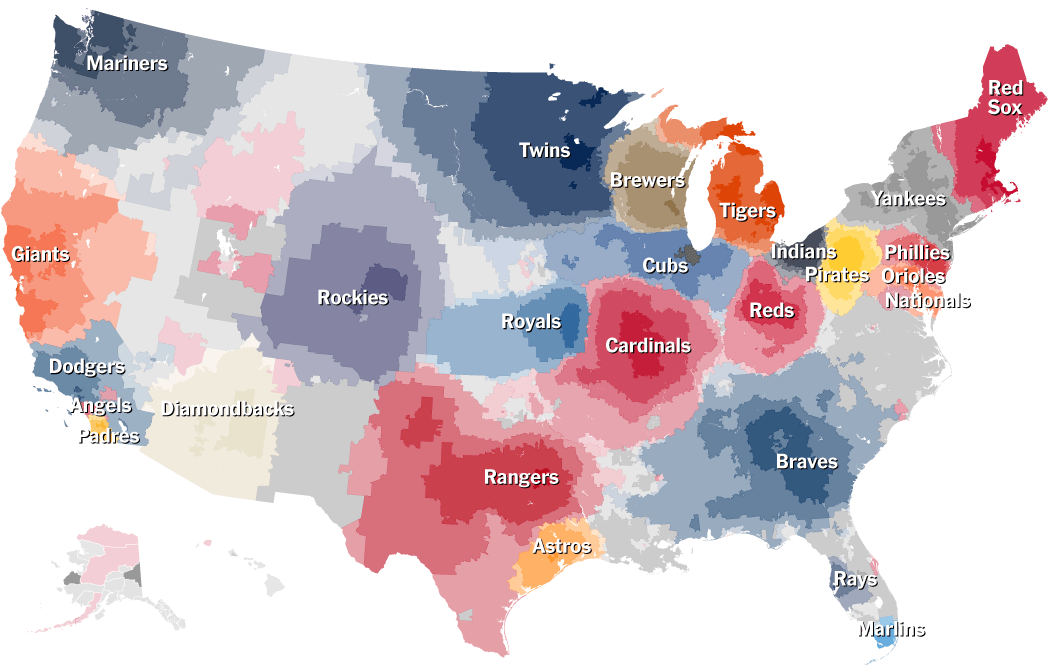
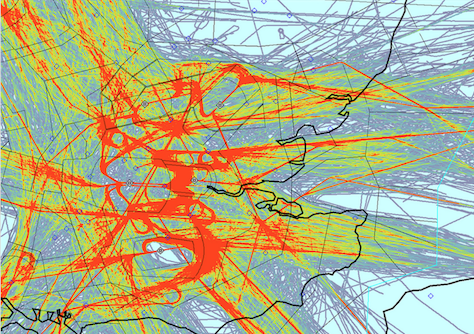
Incorporating Interests with Geopgraphy: NYT Geography of baseball fandom

NYT

Facebook Distribution of baseball team fans
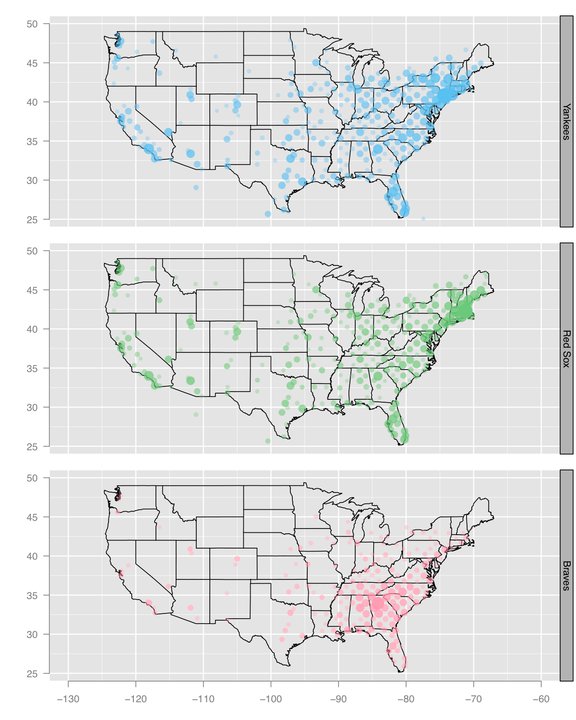facebook

COMPARISON: These two heat map examples depict data gather from facebook about where baseball team fans are geographically located. The two visuals serve different purposes. The NYTs is focusing on the transitions between large team territories as compared to Facebook's visualization of team fan distribution across the country. Regardless of intent, I find the NYT graphic to be richer in content and use the heat map technique to greater effect.

BAD EXAMPLE: Reddit Interest Network
This infographic depicting the frequency of subreddits with the frequent re-posting in red and the less frequent in blue.

reddit

This graph highlights the importance of having a known geography to map information on.

BAD EXAMPLE: Understanding What Emotions Goes Viral for Marketing Campaigns

emotion

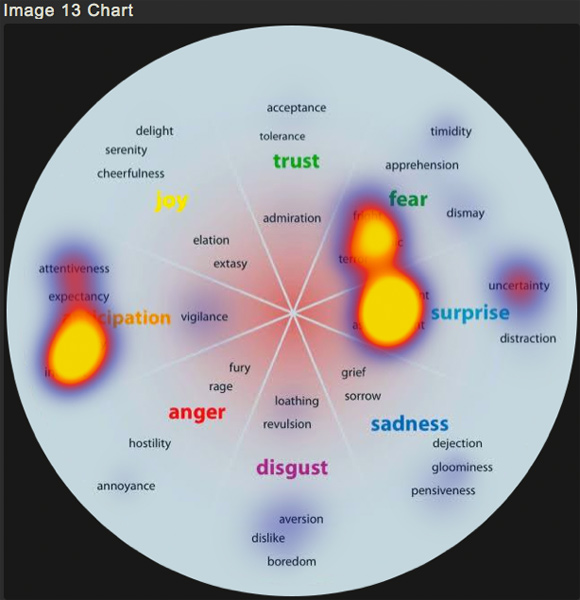
permutation matrix

Bertin's sortable bar charts for the display of multi-dimensional data

features

• Allows arrangements to transform initial matrix - can rearrange rows/columns to reveal information of interest.
• Visual comparison of data to reveal or prove insights.
• Custom organization of data help communicate insights with efficiency.
• Work flow:

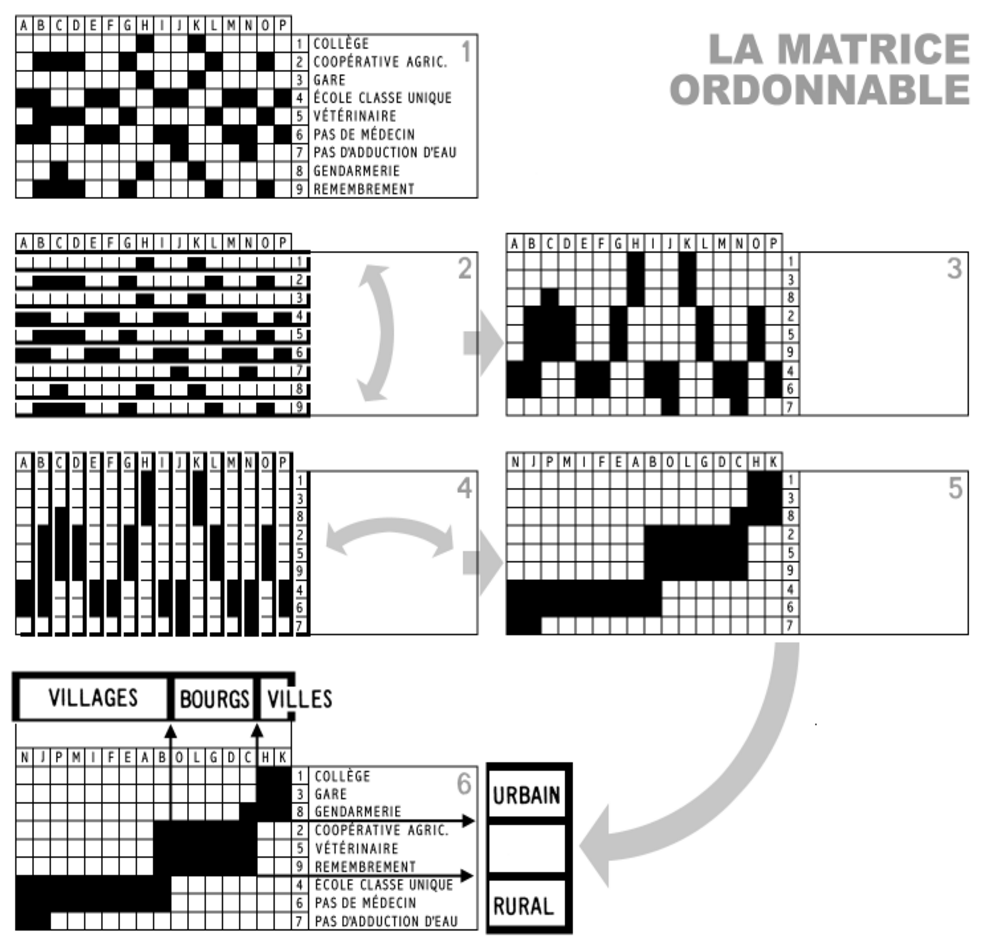
examples

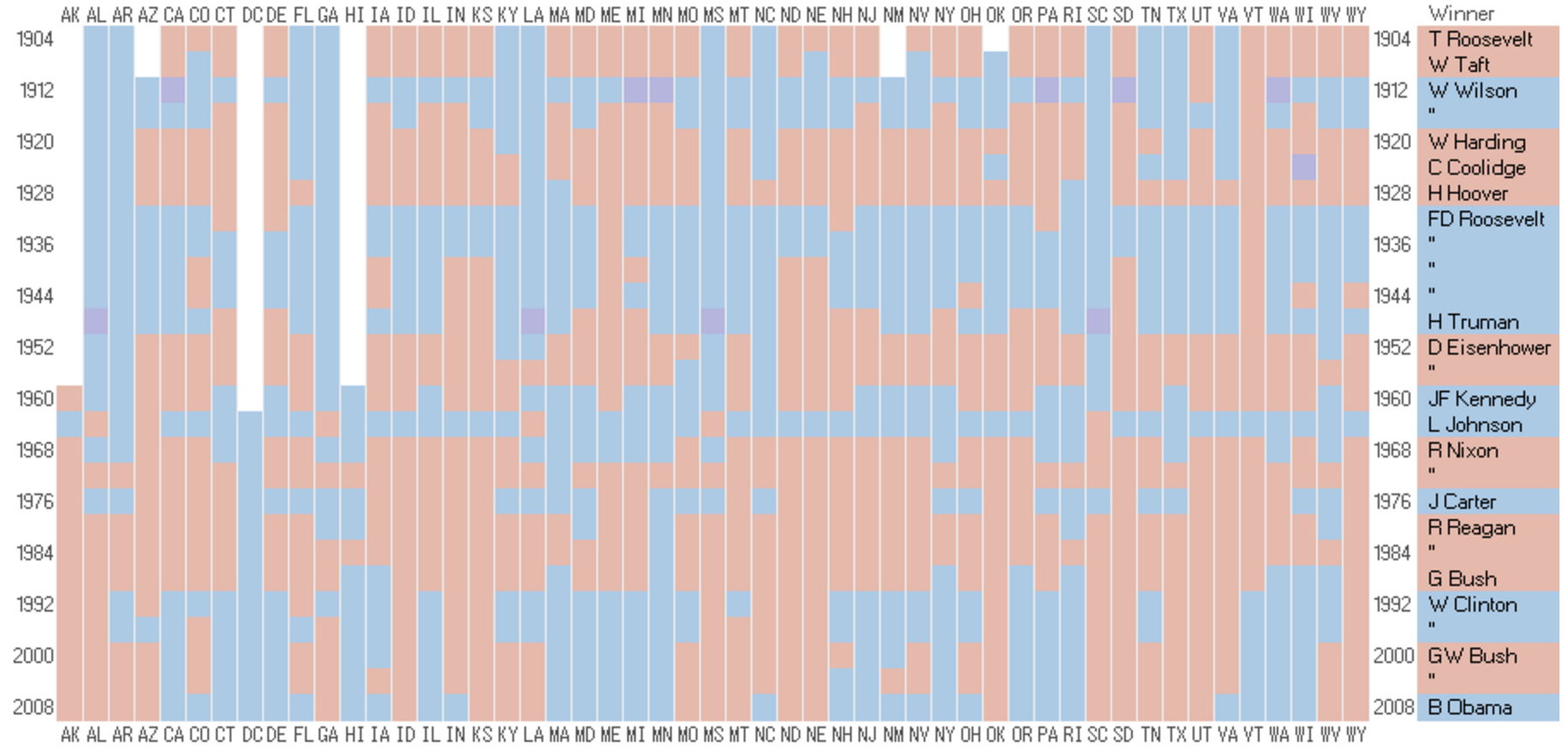
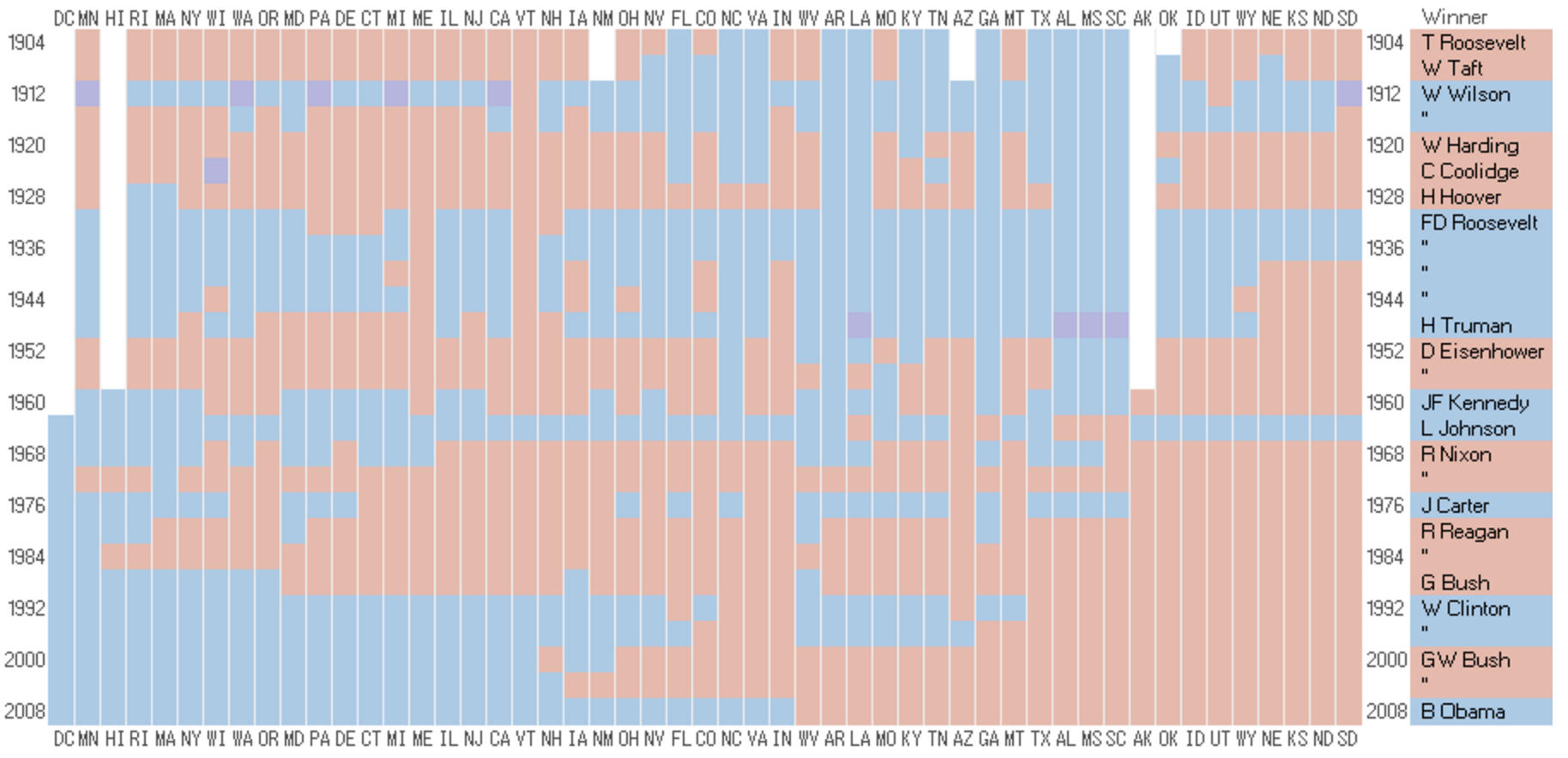
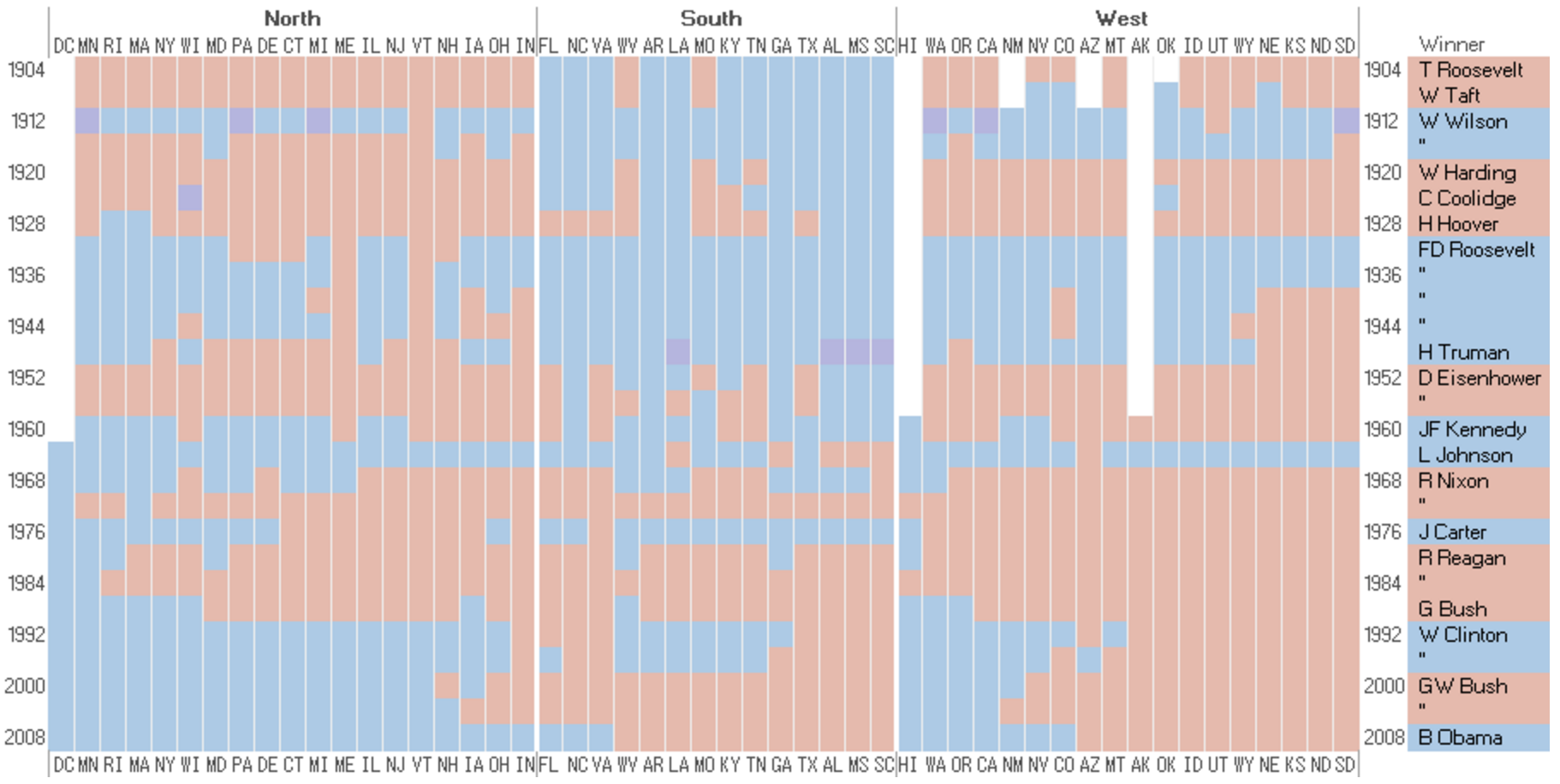
• Results for US Presidential Election Sorting into chronological order reveals a pattern (image 2) and ordering the into three regions shows a clearer picture (image 3) ![]

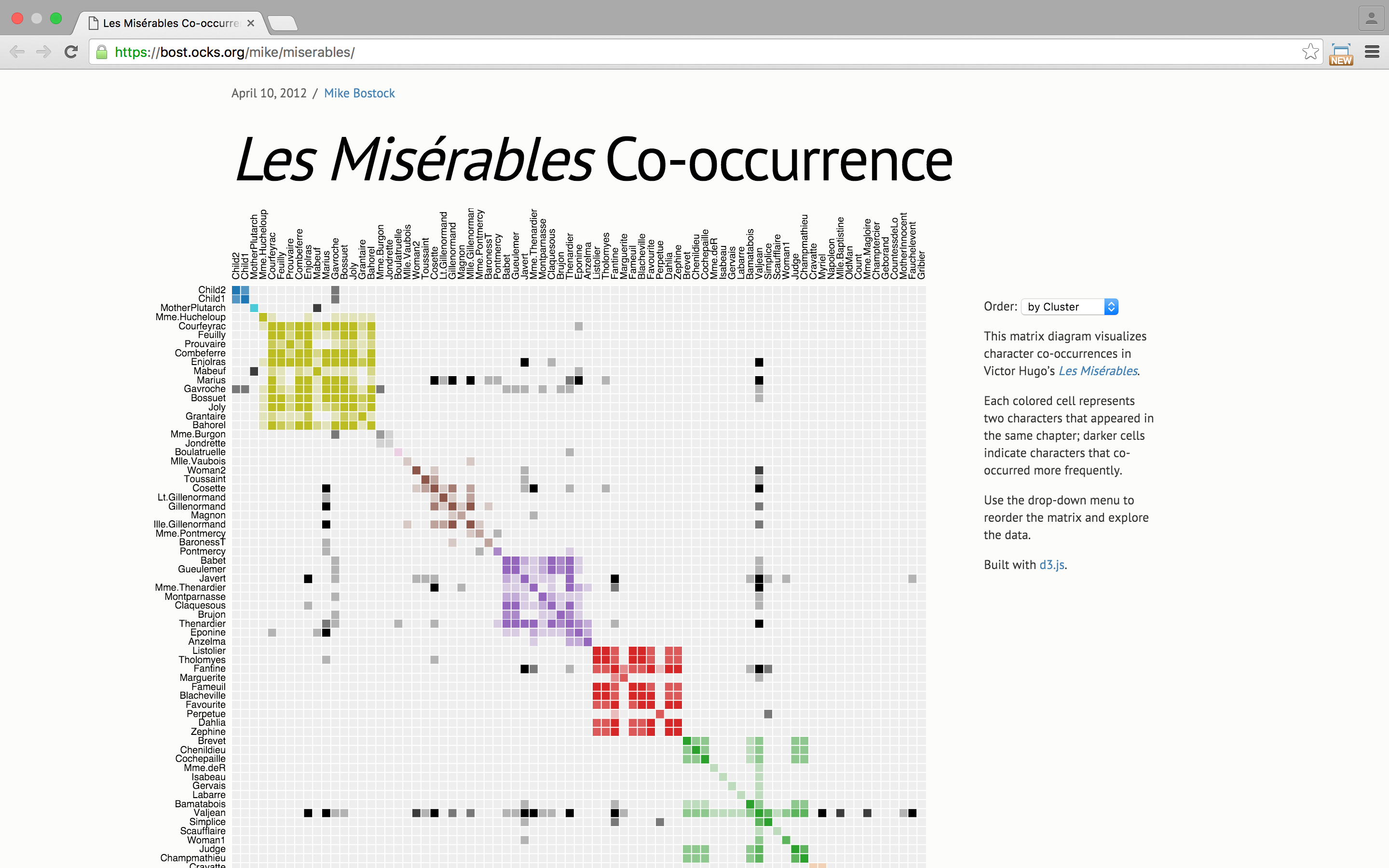
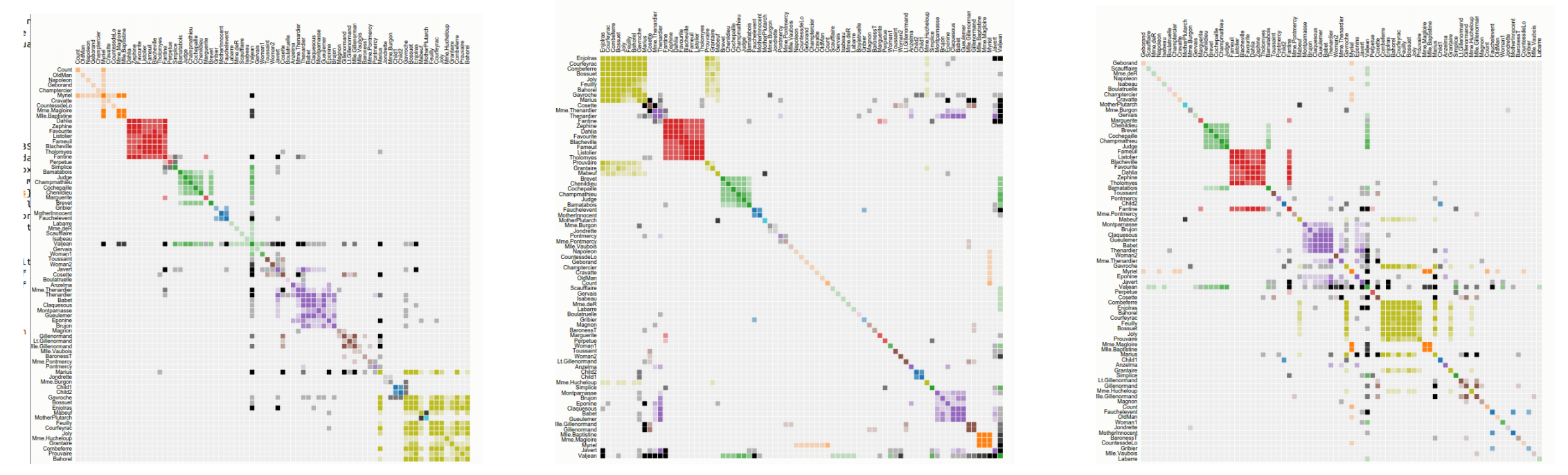
• Reorderings of the Character-appearances Network in Victor Hugo's "Les Miserables"

• Heat Map

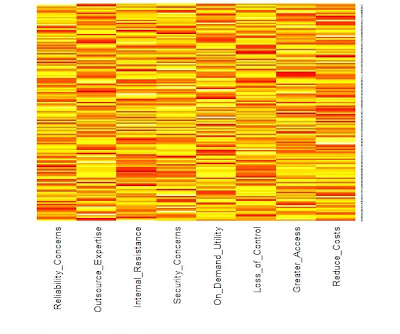
• Hotel Occupancy Within Two Years Highlighted bars represent a value above a certain threshold. Indexing is arbitrary.

• 

Tree Maps

A tree map is an area-based visualization for a hierarchically-ordered (tree-structured) set of data. It is presented as nested rectangles whose relative size and color each convey a dimension of the data.

Here is a visualization of soft drink preferences across a set of people.
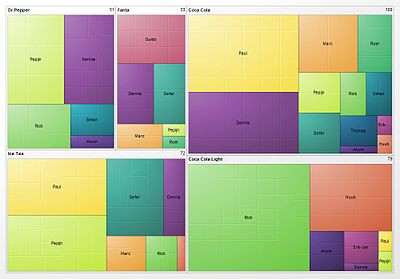Source: Wikipedia

Tree maps are good for quickly seeing whether or not there is a pattern between two dimensions of a data set. The tetris-like geometry also makes Treemapping good for displaying especially large sets in one view.

Creating a tree map involves choosing two dimensions of the data, color-coding one dimension and defining a "tiling algorithm" for the dimension represented by area. The tiling algorithm determines how the rectangles are sub-divided into rectangles of specific area (corresponding to the data). Tree maps are most legible when the area of sub-rectangles have an aspect ratio close to one.

While not the most beautiful example, the following tree map of greenhouse gas emissions by buildings on the campus of the University of North Carolina at Chapel Hill, shows what is meant by "sub-rectangles".

Source: blogs.sas.com

Another good example, and description of how to read it:

"For UNAIDS (the Joint United Nations Programme on HIV/AIDS), Michael Lindsay of studiovertex designed a pair of treemaps that detail the prevalence of HIV worldwide. The first treemap (left side of the above) visualizes the status of those living with HIV (new infections vs. fatalities; those receiving treatment vs. those waiting for treatment). The second treemap (right side) depicts the geographic regions where those with HIV live, drawing attention to the disproportionate incidence of HIV in Sub-Saharan Africa and Asia as compared to the United States and Western Europe." (Source: arcadenw.org)

Bad example 1:
Ungrouped colors make it hard to compare area

Bad example 2:
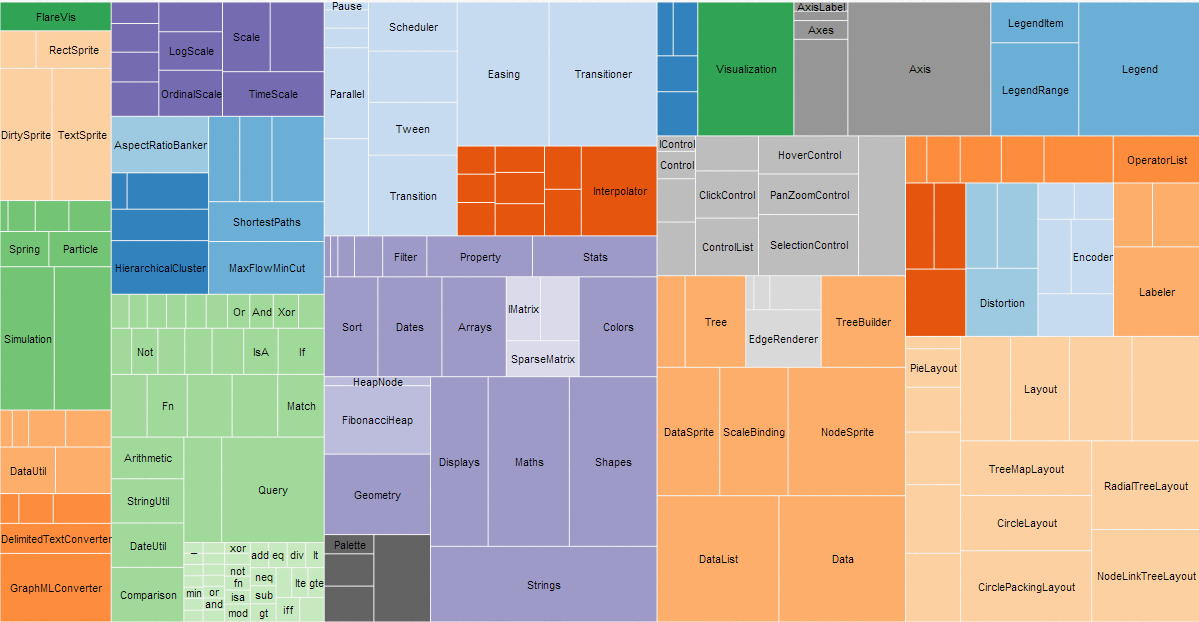Unlabeled groupings with no key

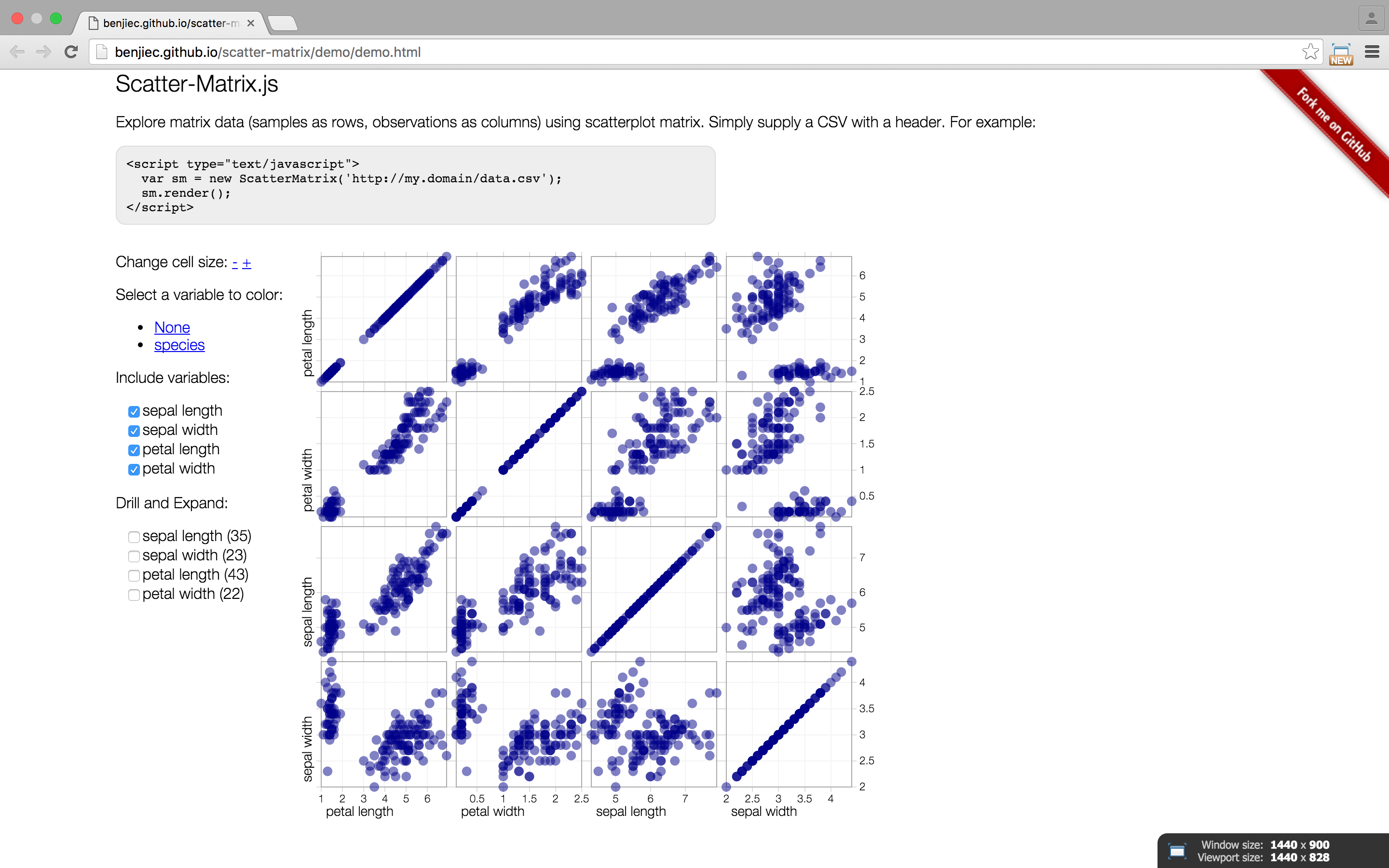
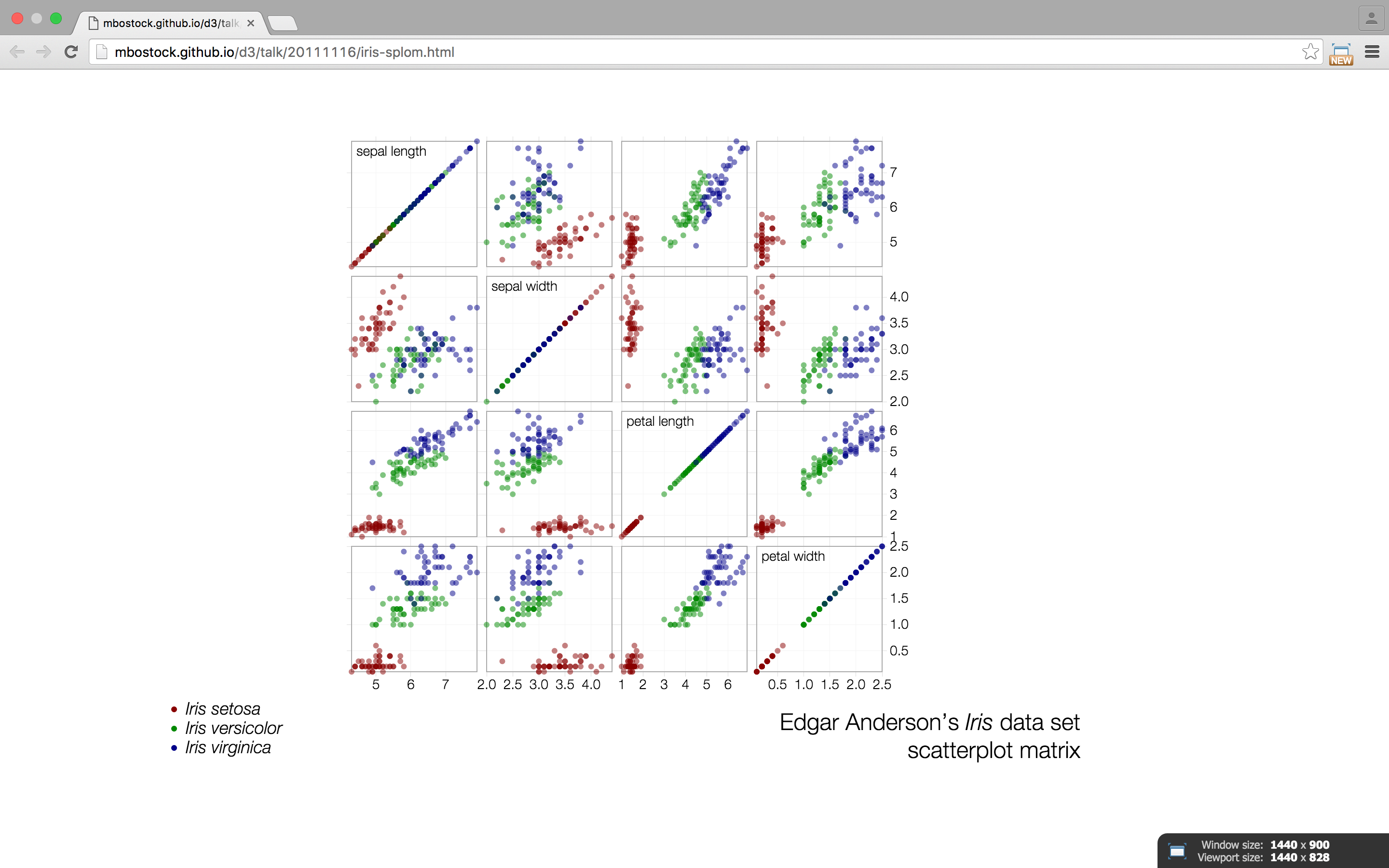
matrix

any two dimensional set of numbers, colors, intensities, sized dots, or other glyphs

good for plotting and analyzing a wide range of data. used arranged in rows and columns and often used in sciences.

there are several types of matrices, including numeric, linear, scatterplot, dot correlation, reorderable, etc...

examples

Chernoff Faces

Chernoff Faces are a way to visualise many different variables at once. Invented in 1973 by Herman Chernoff (who studied applied mathematics at Brown), they are based on the premise that humans are very good at recognising minute changes in faces. Each measurement of the face, including eye width, head height, distance between mouth and nose and many others, can be mapped to a particular variable. Chernoff faces are therefore a type of glyph, a graphical object whose properties represent data values.

Some features (e.g.: eyebrow slant and eye size) carry more perceived importance, so care must be taken when choosing which variables to assign to which features. Note that this will vary hugely from person to person, causing major differences in how two people interpret the data.

Chernoff faces can be plotted as points on Cartesian co-ordinates, with X and Y as the two most important variables and the features filling in the other details. In 1981, Bernhard Flury and Hans Riedwyl suggested maing the faces asymmetrical, thereby doubling the amount of data that could be stored on each face, but also ruining the basic premise of it being a face.

The main issue with this technique is that its fundamental principle, that face recognition can help us see subtle data changes, isn't true. Our ability to recogise faces is a preattentive capability, and does not assist at all in comparison between different faces, which is a serial search task.

Another huge problem with this method is that one personifies the faces in completely inaccurate ways. A downturned mouth may simply mean that an baseball coach used more pinch hitters, but we will always read it as anger or sadness. One ends up making arbitrary assumptions that are not seen in the data. It can be particularly dangerous when facial proportions result in racial stereotypes being read into the visualisation.

This method is fun, but great care is needed, and there may well be a better method.

Crime data from all the states of the US as Chernoff faces. It looks like the data used here was not appropriate to the technique, as the faces have come out very similar looking. The key is also extremely difficult to use.

A good example of how meaningless these are without a key.

Created using 18 different variables, these tests show the maximum, minimum and average faces.

Be careful about colour.

It has been noted that Chernoff faces work better for negative associations than positive.

Isosurfaces

Isosurfaces can be used to create data maps that resemble topographies in 2D or 3D. They have traditionally been used in mathematics, engineering, and medical fields to represent heat distribution, fluid dynamics, or surface qualities of everything from equations to human bones. Water turbulence around a propeller, airflow around a spacecraft reentering the atmosphere, or (as seen below) building ventilation and heating can all be represented this way.

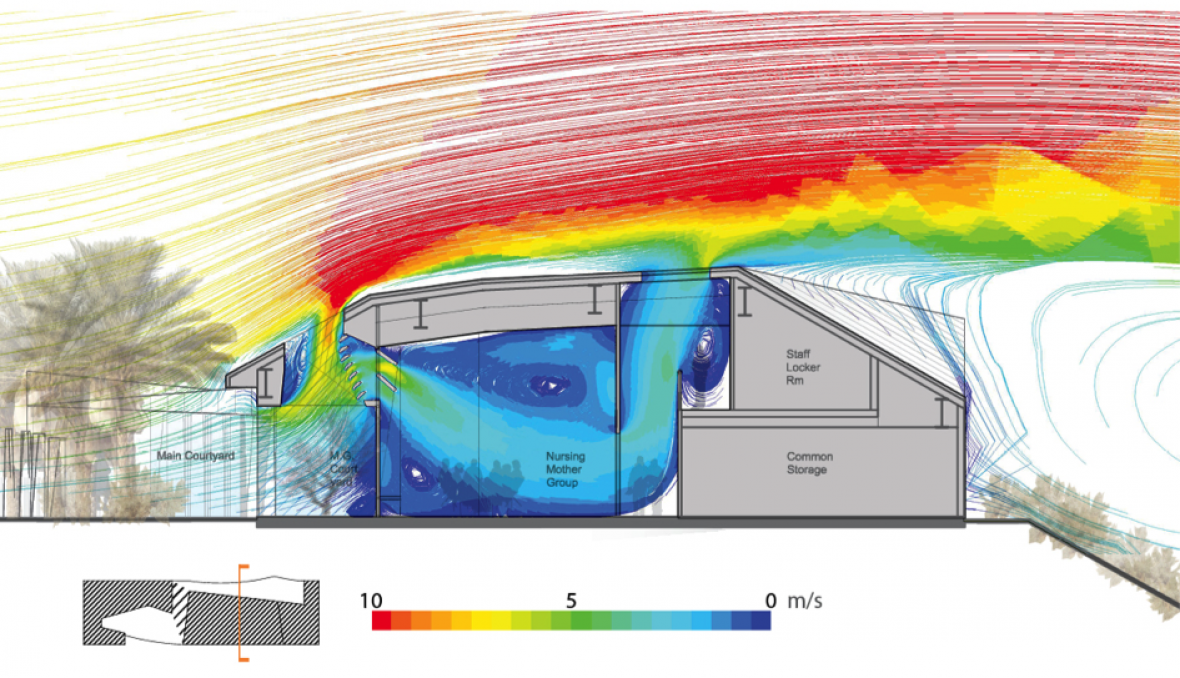Air velocity around and within a naturally-ventilated building

Passive-solar heat distribution within a lecture hall

While these visualizations can be very useful, they can also become confusing very quickly if colors and axes are used indiscriminately...

...or if the relationships depicted are unlabeled or decontextualized.

This idea of mapping with concentric surfaces, however, can also be used in very elegant ways outside of scientific applications. Interactive isosurface maps seem to have great potential for helping people visualize spatial relationships. This web-hosted map, for example, shows the the distance one can travel by bus from Portland's city center in any given increment of time. (For comparison, this somewhat more confusing map aims to do the same thing for Japan by morphing the geography itself rather than creating a spatial overlay.)

Finally, though I was not able to find examples of this, it may be possible to use isosurfaces to represent information that has both breadth and depth, with size of ring depicting breadth and number/height of rings depicting depth.

Survey Plot / Table Lens

Popularized in the "Table Lens" project from Xerox, these resemble series of bar graphs that can be sorted independently.

What is a survey plot?

We present a new visualization, called the Table Lens, for visualizing and making sense of large tables...The Table Lens fuses
symbolic and graphical representations into a single coherent
view that can be fluidly adjusted by the user. This fusion and
interactivity enables an extremely rich and natural style of
direct manipulation exploratory data analysis. — Table Lens

A survey plot is a simple multi-attribute visualization technique that can help to spot correlations between any two variables especially when the data is sorted according to a particular dimension. Each horizontal splice in a plot corresponds to a particular data instance. The data on a specific attribute is shown in a single column, where the length of the line corresponds to the dimensional value. When data includes a discrete or continuous class, the slices (data instances) are colored correspondingly. via Orange

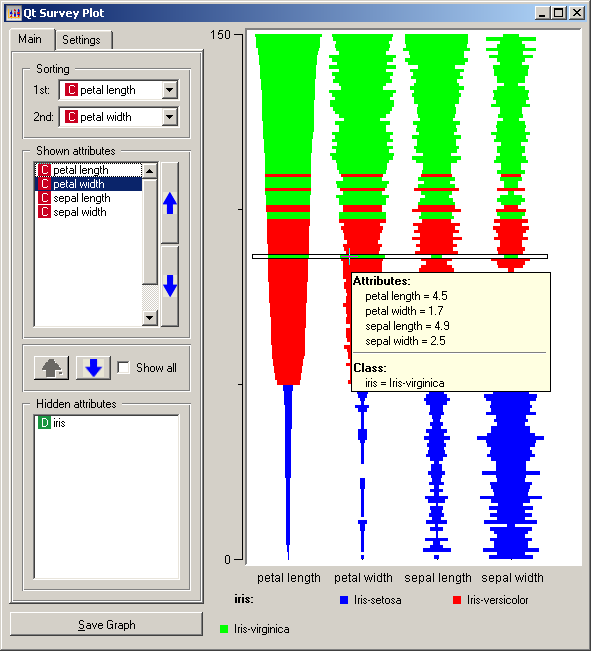
What is it for?

Survey plots can be useful in data analysis to quickly find correlations and patterns in large amounts of data. Not so great if you want to see individual values, it's more of a "bigger pictures" graphing technique.

Compresses larges quantities of data into an easily digested visual. For example, a baseball statistics table contains 323 rows by 24 columns = 7429 cells total which would not fit onto a standard screen. However using the table lens, you could easily display all the data with more room to spare (see below).

Graph

A graph is a collection of nodes and edges representing some sort of objects and their relationships with each other.

Metro Maps are a more practical application of maps. Nodes represent stations and edges represent lines from one station to the next.

Clustering in Social Networks

Traveling Salesman is a famous problem in graph theory whereby given a list of cities and their distances to each other, we want to find an optimal path to pass through every city.

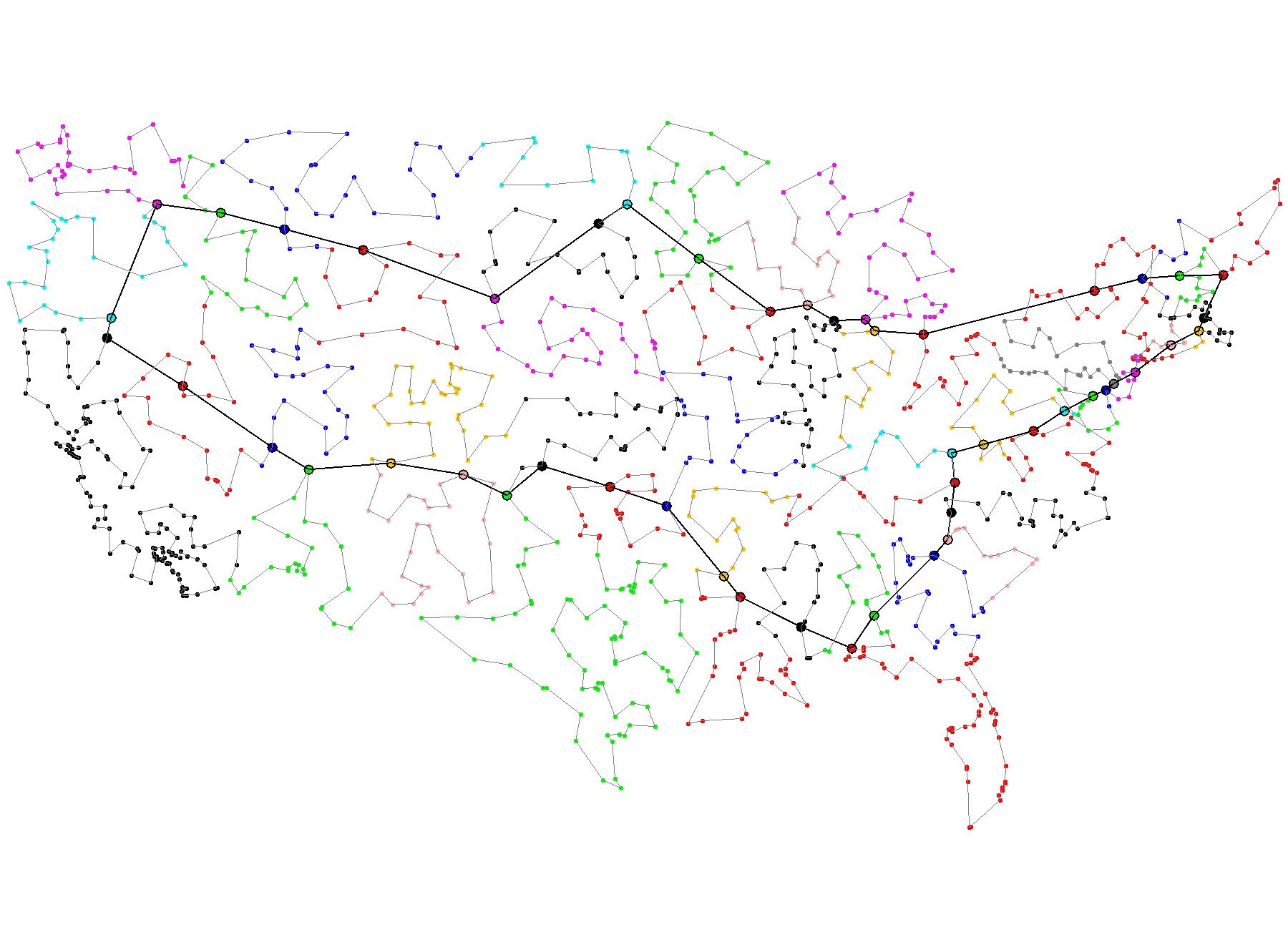
3-Dimensional Graph

Bad Graph

Trees

Trees are a more restrictive type of graph whereby cycles are not allowed to exist.

Syntax trees divide sentences into word nodes based off of their part of speech, revealing their underlying syntactic structure. Simplistic versions of syntax trees such as the Reed-Kellogg diagram below are used to teach children grammar.

An abstract syntax tree (AST) are used within programming languages to parse and compile code.

Tries are a type of trees where each node represents a single character or letter. Following a path starting from the root of the tree to any given leaf will result in a valid word. Tries can be used to store and find patterns in DNA or protein sequences.

L-systems are a system of rules that play out recursively to construct some kind of geometric structure. The tree is more so a representation of this recursion than it is a data structure.

Good/Bad diagram?

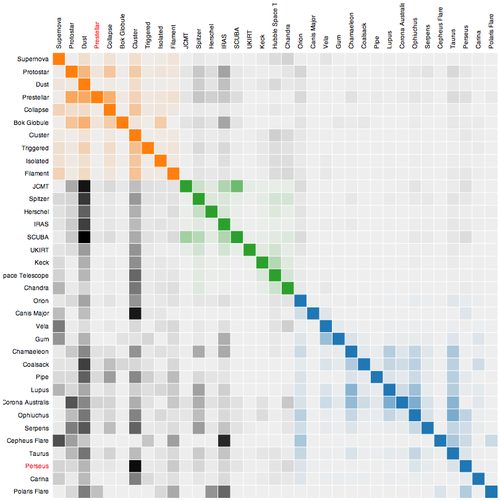
Half Matrix

Where only half a matrix is shown, usually used for similarities, or where two items are being compared against one another (i.e. the D' table). Only half the matrix is needed because it is the same when reflected across its diagonal

• Les Misérables Co-occurrence Matrix

• matrix+scatter plot

• Another version of that last example

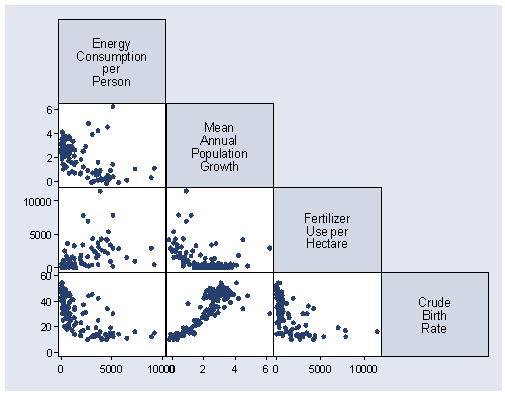
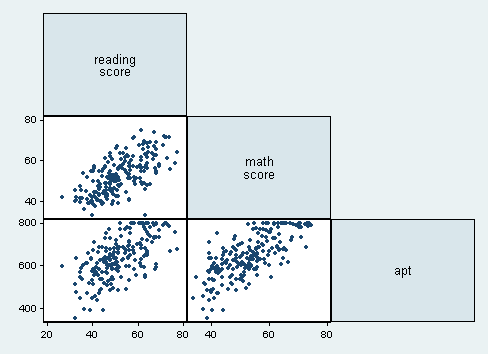
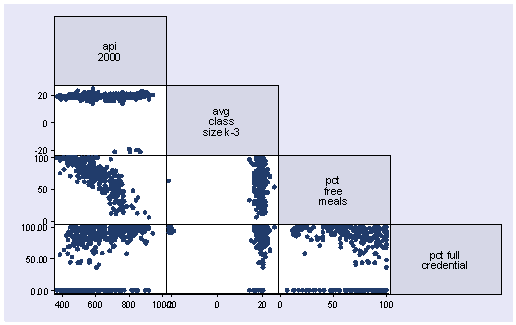
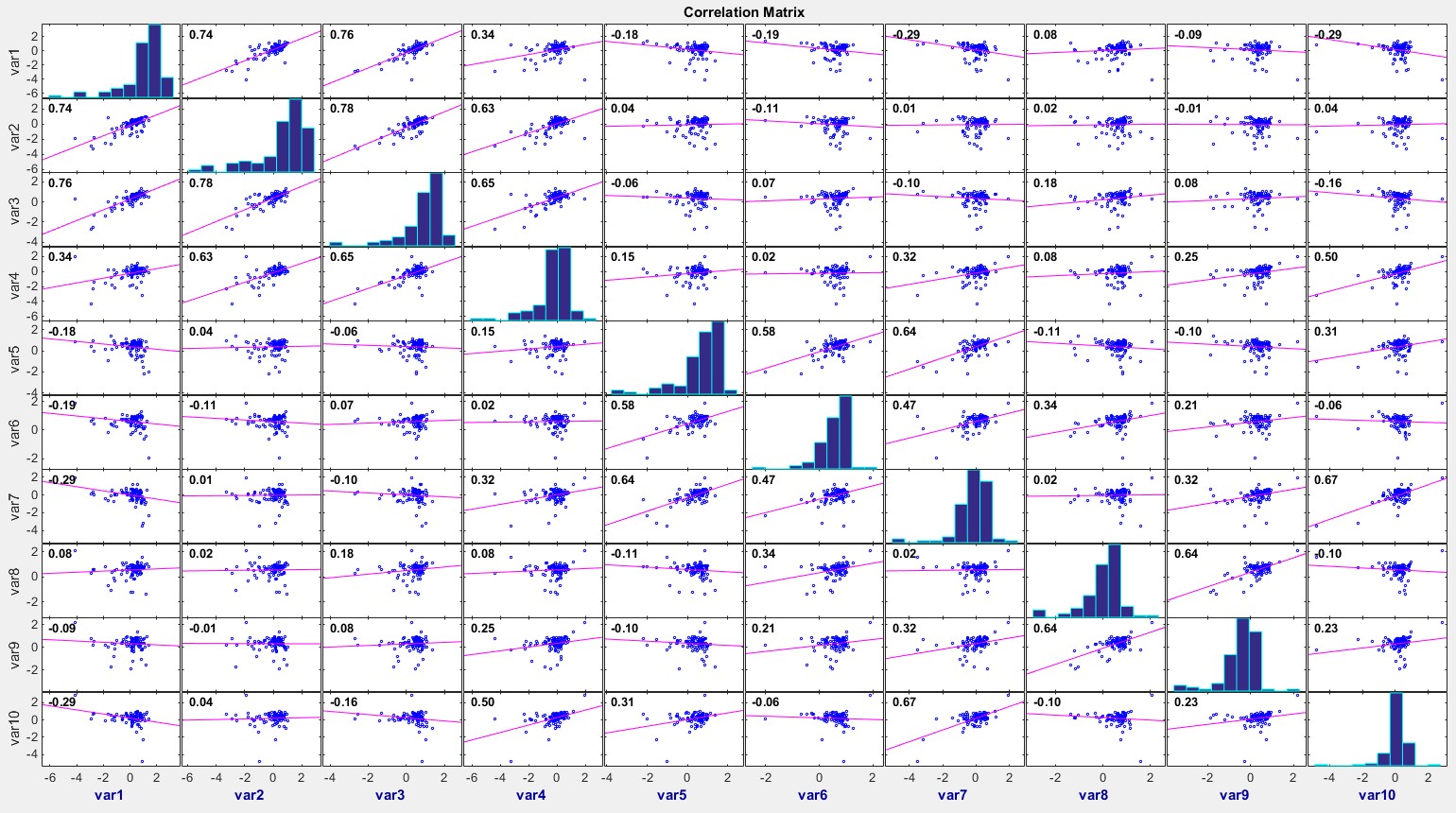
What its good for

• Comparing multiple sets of two items against one another.
• Matrix graph without the redundancy...?
• Visualizing frequency between two matching sets

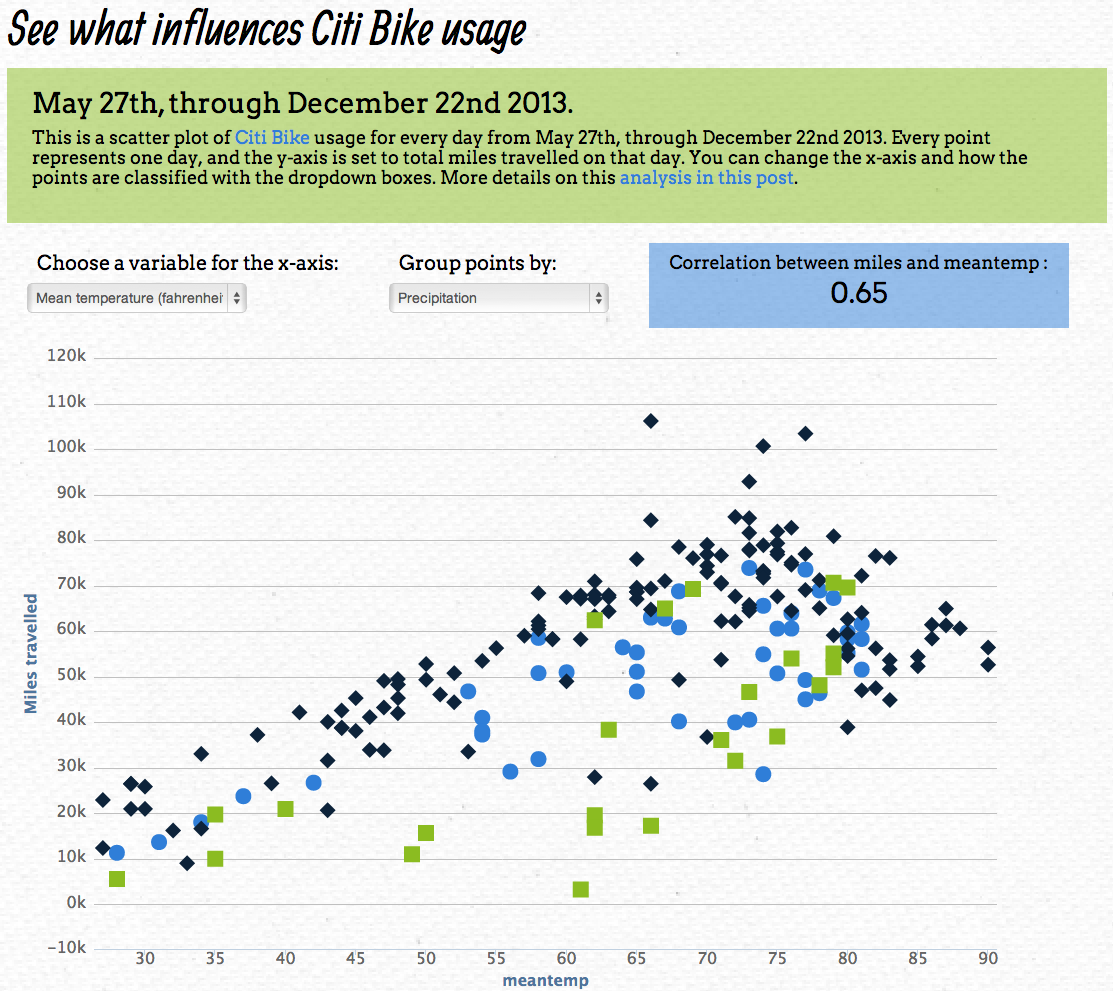
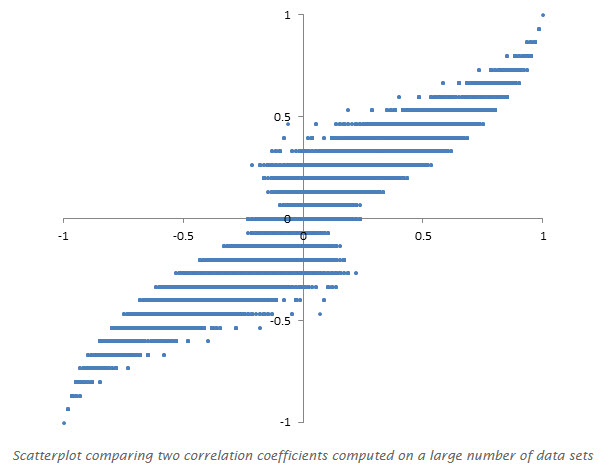
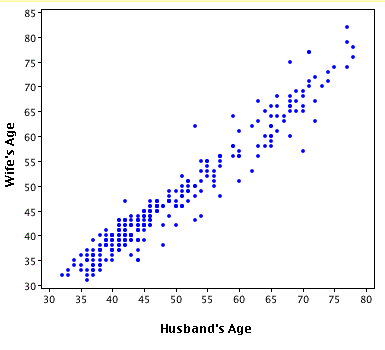
Scatter Plot- The Good, The Bad, and The Ugly

The Good

http://d1oi7t5trwfj5d.cloudfront.net/af/93c8d0e24e11e1baf122000a1d0930/file/meryl%20streep%20matrix.jpeg

Other than being just funny, I think this scatter plot is working because the points/faces are relational to create understanding versus being associated solely to the axis.

http://d1oi7t5trwfj5d.cloudfront.net/af/93c8d0e24e11e1baf122000a1d0930/file/meryl%20streep%20matrix.jpeg

This plot is addressing the magnitude with different colors and shapes which creates more clarity in my opinion.

http://linkit.kr/charts/assets/images/samples/nvd3/2.png

This plot is working similarly to the previous plot in that way as well.

http://coffeespoons.me/wp-content/uploads/2015/05/scatterPlot.png

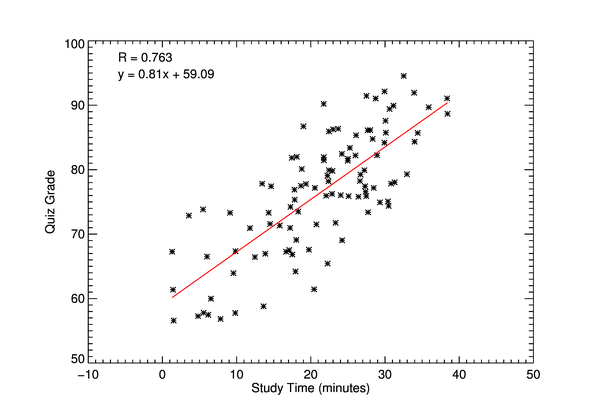
The Bad

http://coffeespoons.me/wp-content/uploads/2015/05/scatterPlot.png
This plot has a lot of variables, while it isn't terrible, I think that because some companies are highlighted and for different characteristics, it is minimizing the readability for the facts that are presented.

https://datavizblog.files.wordpress.com/2013/11/scatterplot-measuring-metrics.jpg

This has the same issues. While the info may have translated into this graphic without intention, the lack of data (too large a gap in the axis increments) makes it too vague to follow.

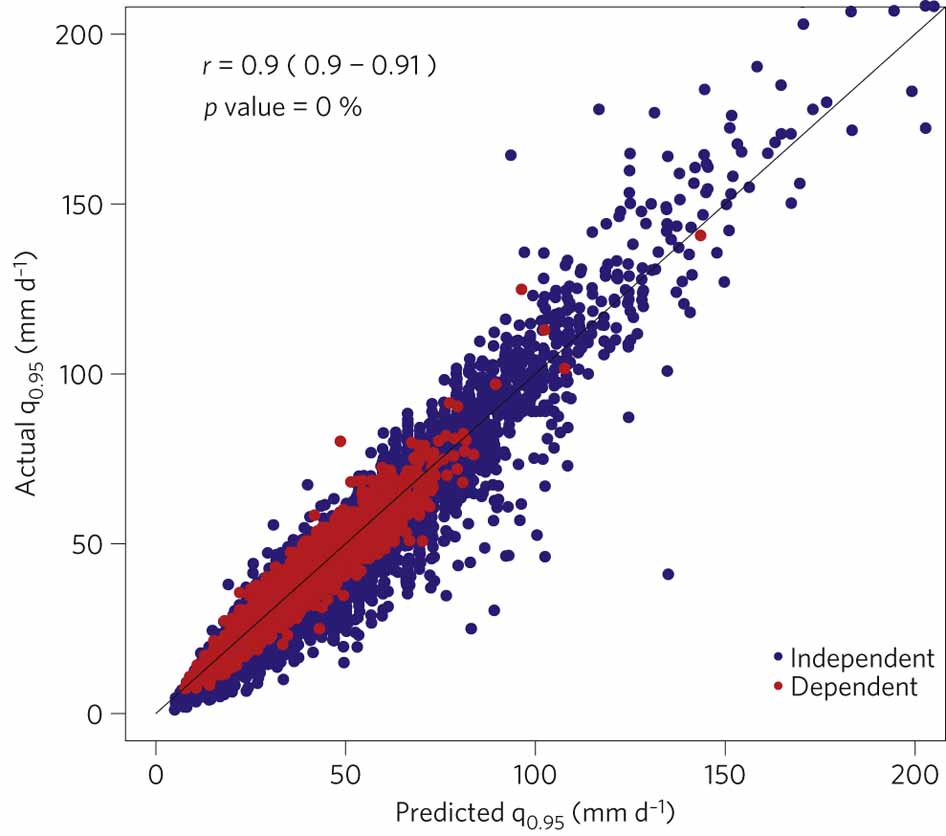http://www.nature.com/nclimate/journal/v2/n7/images/nclimate1497-f3.jpg
The overlap in this graphic is distracting but it might be okay.

The Ugly
http://1.bp.blogspot.com/-OQxk_34rwT8/Ta4aJ0MYBRI/AAAAAAAAAVc/43EPPYdx5uI/s1600/scatterplot.gif

http://www.idlcoyote.com/cgtips/scatter2d1.png

Synthesis:

Scatter Plots have the ability to display large amounts of data in a small field to visualize a potential trend. However, in my naïve opinion, they also seem to leave too much room for inaccuracy. Visually it can be hard to see where points would fall compared to the axis lines and when data overlaps, information gets lots. Some of the better scatter plots are addressing this with different symbols and colors but I still believe it is confusing. Scatter plots can easily become ugly too because their success is related to their simplicity (or really well made graphic design).

Pretty good example:

The first map shows urban transit systems in North America. The map covers a continental space, so it is easy to compare size of transit systems of North America's largest cities. Mexico City and New York City's maps are much more compact and entangled, whereas San Francisco's system is made up of less lines but longer and less compact.
Also good example:

http://darksitefinder.com/maps/world.html

the third is an interactive world map of light usage

Not a very good example:

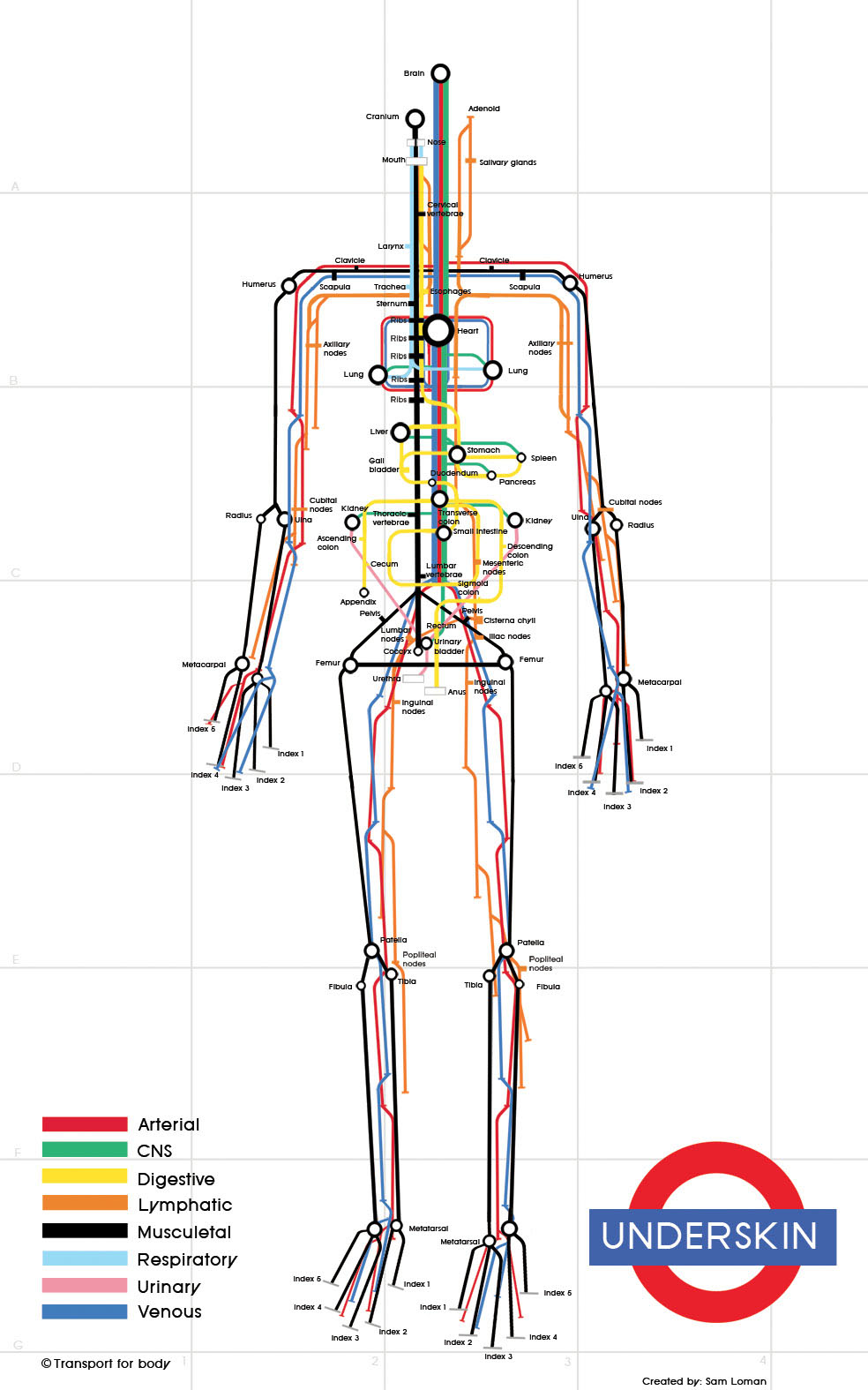
The second map traces 8 different systems of the human body in a subway-like format. The colors of the different systems in the body help visualize the different routes within the body; however, the map oversimplifies the entire system of the body, making each system seem to be separate and distinct. It also downplays the human body's physical complexity.

not so good map:

https://blog.twitter.com/2013/the-geography-of-tweets

Interesting to see the usage of social media on a map and the comparisons between different cities, but the map was only of geotagged tweets and also public tweets, so data can be misleading. I really like being able to see this data on a detailed geographical map, but what is the importance of tracking tweets.

Histogram

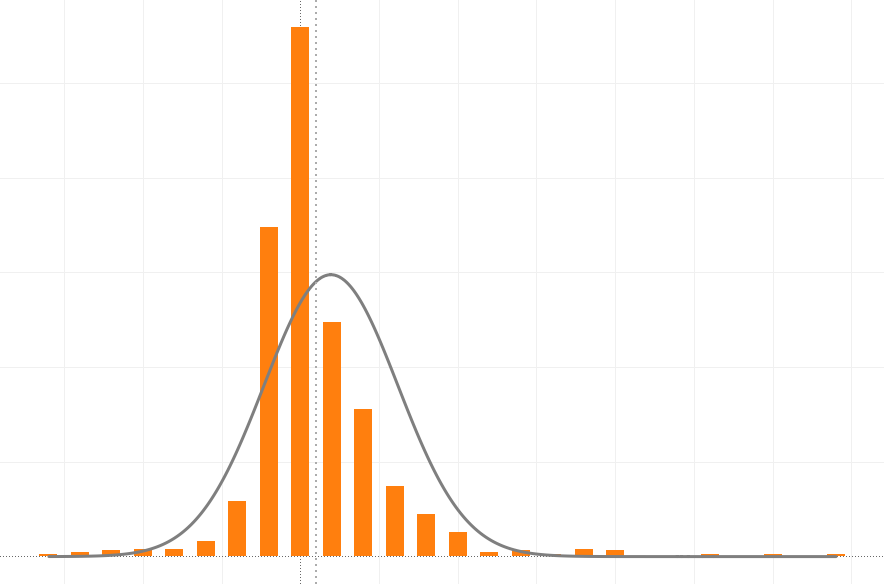
Histogram is a graphical representation of the distribution of numerical data. It is similar to a Bar Chart, but a histogram groups numbers into ranges, and one decides what ranges to use. It's particularly useful when there are a large number of observations.

Example:

Photography Histogram

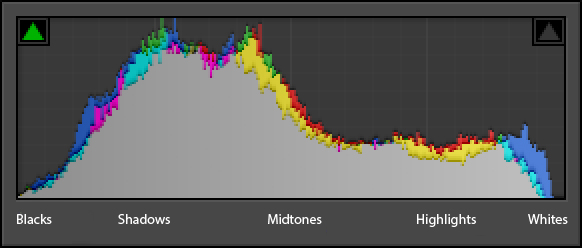
A photography histogram is a graphical representation of the pixels exposed in your image. The left side of the graph represents the blacks or shadows, the right side represents the highlights or bright areas and the middle section is mid-tones (middle or 18% grey). How high the peaks reach represent the number of pixels in that particular tone. Each tone from 0-255 (0 being black and 255 being white) is one pixel wide on the graph, so imagine the histogram as a bar graph all squished together with no spaces between each bar.

Manipulating Histogram

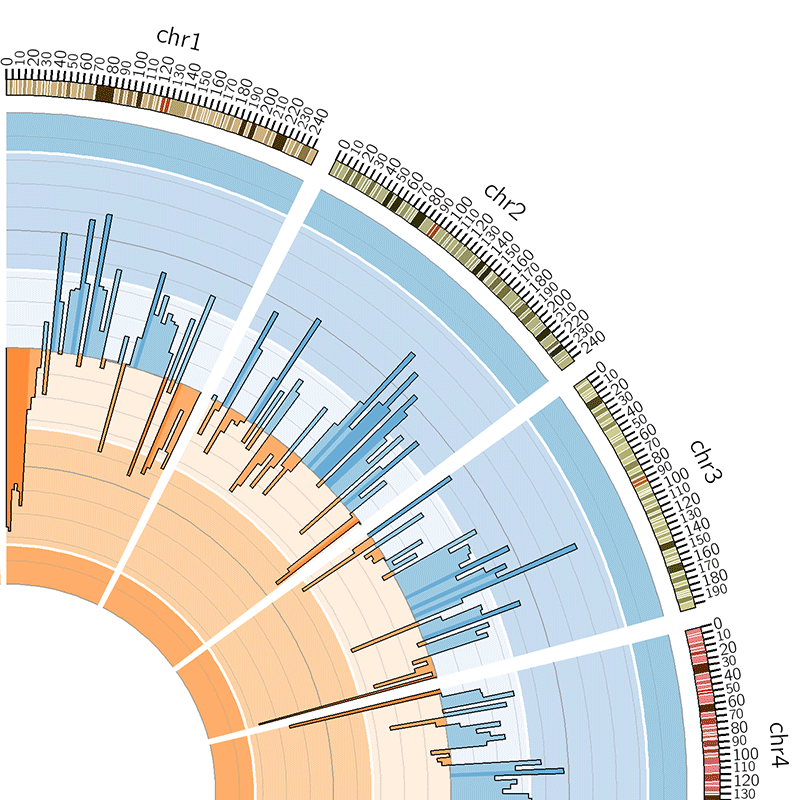
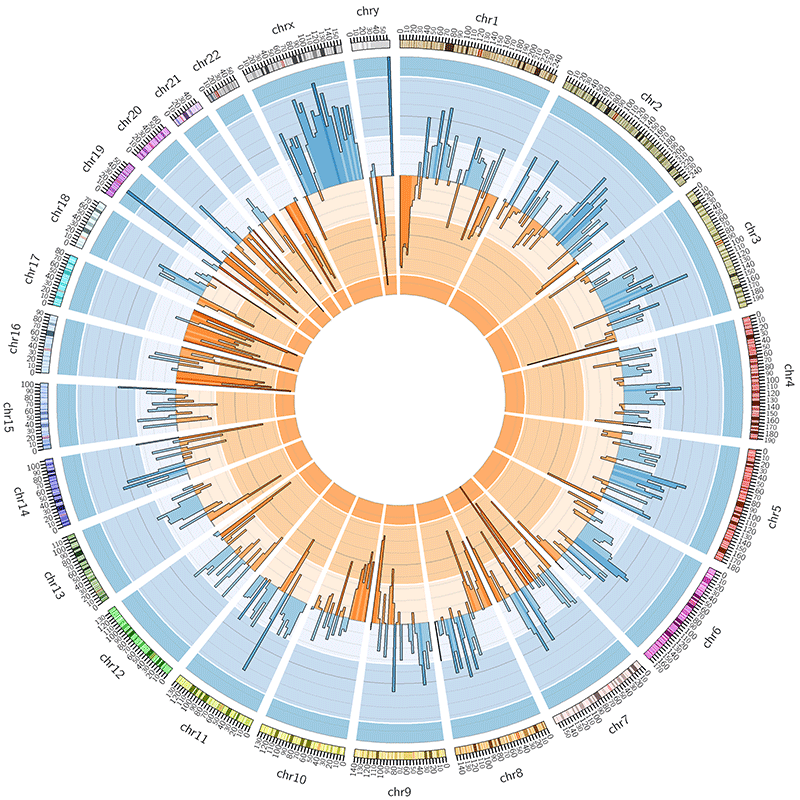
A histogram also can be manipulated and become more complex.

Bad Example:

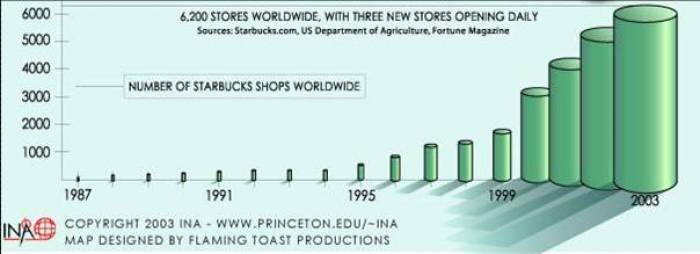
This visualization example is taken from International Networks Archive of Princeton University, a research center of the mapping of Globalization. In this case, the 3-Domain histogram shows the number of Starbucks shops worldwide, which is increasing dramatically in the recent 20 years. Yet the third dimension of the histogram is unnecessary. According to the encoding rules, univariate data should use 2-Domain plot. For example, according to the exact number of Starbuck shops in 1996 and 2003, the volume of the cylinder of the former should be 1/6 of the later, which is much smaller than the actual cylinder of 2003. Also, the shade of the cylinder is confusing.

Also, when the ranges of the graphs are too broad, it's difficult to compare or can fail giving information.